【题目】如图,表示甲、乙两同学沿同一条路到达目的地过程中,路程S(千米)与时间t(小时)之间关系的图象,根据图象中提供的信息回答问题:
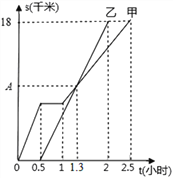
(1)乙的速度为_______千米/时;
(2)两人在乙出发后________小时相遇;
(3)点A处对应的数字为_________;
(4)甲在出发后1小时至2.5小时之间的速度为_________千米/时.
参考答案:
【答案】 12; 0.8 9.6 7
【解析】分析:(1)由图象获取乙运动的路程与时间代入速度公式求解即可.
(2)行程问题的函数图象中的交点表示两个运动对象相遇,该点的坐标表示相遇的时刻及行驶的路程.(3)A点对应的数表示甲乙二人相遇时他们的行程.(4)求出1小时的时候甲的行程,然后求出所求时段及该时段的路程代入公式求解即可.
本题解析:
(1)由图象可得,
乙的速度为:18÷(20.5)=12千米/小时;
故答案为:12
(2)∵两图象的交点表示二人在同一时刻在同一地点,即二人在途中相遇,且1.30.5=0.8(时)
∴两人在乙出发0.8小时相遇。
故答案为:0.8
(3)∵点A处对应的数字表示二人相遇是随行路程,
由(1)知乙的速度为12千米/小时,
∴12×0.8=9.6(千米)
故答案为:9.6
(4)∵甲在出发后1小时至2.5小时之间运动的路程s(千米)与时间t(小时)之间关系的图象是一条线段,
∴设其解析式为y=kx+b,
则: ![]() 解之得:
解之得: ![]() ,
,
∴y=7x+0.5
∴当x=1是,y=7+0.5=7.5,即1小时的时候甲行驶的路程为7.5千米
∴甲在出发后1小时至2.5小时之间的速度为:(187.5)÷(2.51)=7(千米/时).
故答案为:7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式x2+ax+b分解因式,得(x+1)(x-3)则a , b的值分别是( )
A.a=2,b=3
B.a=-2,b=-3
C.a=-2,b=3
D.a=2,b=-3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式从左到右的变形为分解因式的是( )
A.m2-m-6=(m+2)(m-3)
B.(m+2)(m-3)=m2-m-6
C.x2+8x-9=(x+3)(x-3)+8x
D.18x3y2=3x3y2·6 -
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=x2+6x+5化为y=a(x﹣h)2+k的形式为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)物体向右运动4m记作+4m,那么物体向左运动3m,应记作____m.
(2)单项式﹣
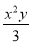 的系数是____.
的系数是____.(3)一个数的倒数是﹣1,这个数是____.
(4)|a|=5,|b|=3,且|a+b|=a+b,则ab=____.
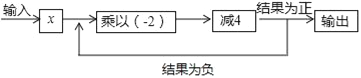
(5)按下列程序输入一个数x,若输入的数x=0,则输出结果为____.
(6)如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“
 ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为__________________.
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为__________________. 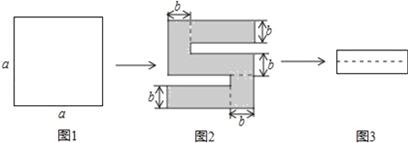
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
十进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如,用十六进制表示:C+F=1B,19﹣F=A,18÷4=6,则A×B=( )
A. 72 B. 6E C. 5F D. B0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2
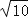 ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.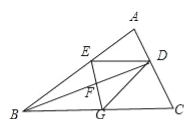
相关试题

