【题目】如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.

(1)求证:BE=BF;
(2)若△ABC的面积为70,AB=16,DE=5,则BC= .
参考答案:
【答案】(1)见解析;(2)12
【解析】
试题分析:(1)由角平分线的对称性直接证明△DBE≌△DBF即可;
(2)先算出三角形ABD的面积,再得出三角形BCD的面积,高DF=DE=5,从而直接算出BC.
(1)证明:∵DE⊥AB,DF⊥BC,
∴∠BED=∠BFD=90°,
∵BD是△ABC的角平分线,
∴∠EBD=∠FBD,
又∵BD=BD,
∴△DBE≌△DBF,
∴BE=BF;
(2)解:∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE=5,
∴![]() ,
,
∴![]() =70﹣40=30,
=70﹣40=30,
∴BC=12.
故答案为12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以原点为中心,把点A(4,5)逆时针旋转90O,得到的点B的坐标为_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】县医院住院部在连续10天测量某病人的体温与36℃的上下波动数据为:0.2, 0.3, 0.1, 0.1, 0, 0.2, 0.1, 0.1, 0.1, 0,则对这10天中该病人的体温波动数据分析不正确的是( )
A. 平均数为0.12 B. 众数为0.1
C. 中位数为0.1 D. 方差为0.02
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索与研究:
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】关于二次函数y=ax2+bx+c的图象有下列命题:
①当c=0时,函数的图象经过原点;
②当c>0,且函数的图象开口向下时,方程ax2+bx+c=0必有两个不相等的实根;
③函数图象最高点的纵坐标是
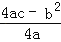 ;
;④当b=0时,函数的图象关于y轴对称.
其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是
A. 两直线与第三条直线相交,同位角相等
B. 两直线与第三条直线相交,内错角相等
C. 两直线平行,同旁内角相等
D. 两直线平行,内错角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在直角梯形ABCD中,AD//BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
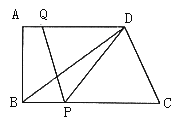
(1)设△DPQ的面积为S,用含有t的代数式表示S.
(2)当t为何值时,四边形PCDQ是平行四边形?
相关试题

