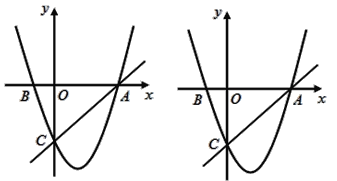
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
参考答案:
【答案】(1)![]() ,
, ![]() ,
, ![]() (2)存在P的坐标是
(2)存在P的坐标是![]() 或
或![]() (3)当EF最短时,点P的坐标是:(
(3)当EF最短时,点P的坐标是:(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )
)
【解析】试题分析:(1)根据题意得出答案;(2)分以点C为直角顶点和点A为直角顶点两种情况分别进行计算;两种情况都根据等腰直角三角形的性质得出点的坐标;(3)根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短,根据OC=OA=3,OD⊥AC得出 D是AC的中点,从而得出点P的纵坐标,然后根据题意得出方程,从而求出点P的坐标.
试题解析:(1)![]() ,
,![]() , (-1,0).
, (-1,0).
(2)存在.
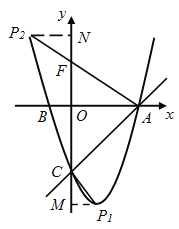
第一种情况,当以C为直角顶点时,过点C作CP1⊥AC,交抛物线于点P1.过点P1作y轴的垂线,垂足是M.
∵OA=OC,∠AOC =90° ∴∠OCA=∠OAC=45°. ∵∠ACP1=90°, ∴∠MCP1=90°-45°=45°=∠C P1M.
∴MC=MP1. 由(1)可得抛物线为![]() .
.
设![]() ,则
,则![]() , 解得:
, 解得:![]() (舍去),
(舍去),![]() .
.
∴![]() . 则P1的坐标是
. 则P1的坐标是![]() .
.
第二种情况,当以A为直角顶点时,过点A作AP2⊥AC,交抛物线于点P2,过点P2作y轴的垂线,垂足是N,AP2交y轴于点F. ∴P2N∥x轴.由∠CAO=45°, ∴∠OAP2=45°. ∴∠FP2N=45°,AO=OF=3.
∴P2N=NF. 设![]() ,则
,则![]() . 解得:
. 解得:![]() (舍去),
(舍去),![]() .
.
∴![]() , 则P2的坐标是
, 则P2的坐标是![]() .
.
综上所述,P的坐标是![]() 或
或![]()
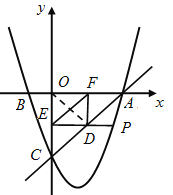
(3)连接OD,由题意可知,四边形OFDE是矩形,则OD=EF.
根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短. 由(1)可知,在Rt△AOC中,
∵OC=OA=3,OD⊥AC, ∴ D是AC的中点. 又∵DF∥OC, ∴![]() .
.
∴点P的纵坐标是![]() 则
则![]() , 解得:
, 解得:![]() .
.
∴当EF最短时,点P的坐标是:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式:
(1) +
+ 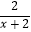 +
+ 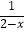
(2) ÷
÷ 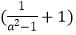 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在日本核电站事故期间,我国某监测点监测到极微量的人工放射性核素碘﹣131,其浓度为0.0000963贝克/立方米.数据“0.0000963”用科学记数法可表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2﹣2x﹣6=0,原方程可化为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接第二届“环泉州湾国际自行车赛”的到来,泉州台商投资区需要制作宣传单.有两个印刷厂前来联系制作业务,甲厂的优惠条件是:按每份定价1.5元的八折收费,另收900元制版费;乙厂的优惠条件是:每份定价1.5元的价格不变,而制版费900元则六折优惠.且甲乙两厂都规定:一次印刷数量至少是500份.
(1)若印刷数量为
 份(
份(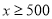 ,且
,且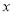 是整数),请你分别写出两个印刷厂收费的代数式;
是整数),请你分别写出两个印刷厂收费的代数式;(2)如果比赛宣传单需要印刷1100份,应选择哪个厂家?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:
①两点确定一条直线;②两点之间,线段最短;③对顶角相等;④内错角相等;
其中真命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).

(1)当t=2时,①AB= ___ cm.②求线段CD的长度.
(2)用含t的代数式表示运动过程中AB的长.
(3)在运动过程中,若AB中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.
相关试题

