【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
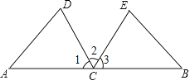
(1)求证:△ACD≌△BCE;
(2)若∠D=75°,求∠B的度数.
参考答案:
【答案】(1)详见解析;(2)45°.
【解析】
(1)先利用角平分线性质、以及等量代换,可证出∠1=∠3,结合CD=CE,C是AB中点,即AC=BC,利用SAS可证全等;
(2)利用角平分线性质,可知∠1=∠2,∠2=∠3,从而求出∠1=∠2=∠3,再利用全等三角形的性质可得出∠E=∠D,在△BCE中,利用三角形内角和是180°,可求出∠B.
(1)证明:∵点C是线段AB的中点,
∴AC=BC,
又∵CD平分∠ACE,CE平分∠BCD,
∴∠1=∠2,∠2=∠3,
∴∠1=∠3,
∵在△ACD和△BCE中,
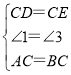 ,
,
∴△ACD≌△BCE(SAS).
(2)∵∠1+∠2+∠3=180°,
∴∠1=∠2=∠3=60°,
∵△ACD≌△BCE,
∴∠E=∠D=75°,
∴∠B=180°-∠E-∠3=180°-75°-60°=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张等边三角形纸片沿各边中点剪成4个小三角形,称为第一次操作;然后将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;……,根据以上操作,若要得到100个小三角形,则需要操作的次数是( )

A. 25 B. 33 C. 34 D. 50
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,当一个点到达终点时另一个点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=______秒时,△PEC与△QFC全等.
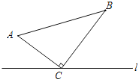
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)2m2-4m+1-2(m2+2m-
 ),其中m=-1;
),其中m=-1;(2)5xy2-[2x2y-(2x2y-3xy2)],其中(x-2)2+|y+1|=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
已知
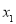 ,
,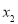 ,
,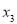 ,…
,…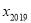 都是不等于0的有理数,若
都是不等于0的有理数,若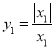 ,求
,求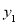 的值.
的值.解:当
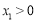 时,
时,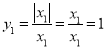 ;当
;当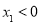 时,
时,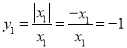 ,所以
,所以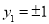 参照以上解答,试探究以下问题:
参照以上解答,试探究以下问题:(1)若
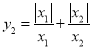 ,求
,求 的值
的值(2)若
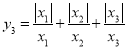 ,则
,则 的值为__________;
的值为__________;(3)由(1)、(2)试猜想,
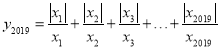 共有__________个不同的值,在
共有__________个不同的值,在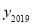 这些不同的值中,最大的值和最小的值的差等于__________.
这些不同的值中,最大的值和最小的值的差等于__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
“十一”黄金周期间,齐齐哈尔市动物园在7天假期中每天接待的人数变化如下表(正数表小比前一天多的人数,负数表示比前一天少的人数):
日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
人数变化(万人)
+1.6
+0.8
+0.4
-0.4
-0.8
+0.2
-1.2
(1)若9月份的最后一天9月30日的游客人数记为
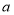 万人,请用含
万人,请用含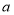 的代数式表示10月2日的游客人数;
的代数式表示10月2日的游客人数;(2)在(1)条件下,请直接写出七天内游客人数最多的是哪天,有多少万人?
(3)若9月30日的游客人数为2万人,门票每人100元,则黄金周期间齐齐哈尔市动物园票收入是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有五张正面分别标有数字﹣2,﹣1,0,1,2的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,0)的概率是__.
相关试题

