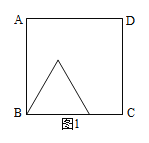
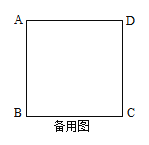
【题目】如图1,图2中,正方形ABCD的边长为6,点P从点B出发沿边BC—CD以每秒2个单位长的速度向点D匀速运动,以BP为边作等边三角形BPQ,使点Q在正方形ABCD内或边上,当点Q恰好运动到AD边上时,点P停止运动。设运动时间为t秒(t≥0)。
(1)当t=2时,点Q到BC的距离=_____;
(2)当点P在BC边上运动时,求CQ的最小值及此时t的值;
(3)若点Q在AD边上时,如图2,求出t的值;
(4)直接写出点Q运动路线的长。

参考答案:
【答案】(1)![]() ;(2)t=
;(2)t=![]() ,CQ=3
,CQ=3![]() ;(3)
;(3) ![]() ;(4)
;(4) ![]()
【解析】试题分析:![]() 过点
过点![]() 作
作![]() 用三角函数的知识即可求出点Q到BC的距离,
用三角函数的知识即可求出点Q到BC的距离,
![]() 点P在BC边上运动时,有
点P在BC边上运动时,有![]() ,根据垂线段最短,当
,根据垂线段最短,当![]() 时,CQ最小,作图,求解即可.
时,CQ最小,作图,求解即可.
![]() 若点Q在AD边上,则
若点Q在AD边上,则![]() 证明Rt△BAQ≌Rt△BCP,
证明Rt△BAQ≌Rt△BCP,![]()
根据![]() 列出方程求解即可.
列出方程求解即可.
![]() 点Q运动路线的长等于点
点Q运动路线的长等于点![]() 运动的路线长:
运动的路线长:![]()
试题解析:![]() 如图:
如图:
过点![]() 作
作![]()

当![]() 时,
时,![]()
![]() 是等边三角形,
是等边三角形,
![]()
![]()
故答案为:![]()
![]() 点P在BC边上运动时,有
点P在BC边上运动时,有![]() ,根据垂线段最短,当
,根据垂线段最短,当![]() 时,CQ最小,
时,CQ最小,
如图,在直角三角形BCQ中,![]() ,
,

![]()
![]()
∴![]()
∴![]()
∴![]()
(3)若点Q在AD边上,则![]()
∵![]()
∴Rt△BAQ≌Rt△BCP(HL),
∴![]()
∴![]()
∵![]() ,且由勾股定理可得,
,且由勾股定理可得,![]()
∴![]()
解得:![]() (不合题意,舍去),
(不合题意,舍去),![]()
∴![]() .
.
(4)点Q运动路线的长等于点![]() 运动的路线长:
运动的路线长:![]()

-
科目: 来源: 题型:
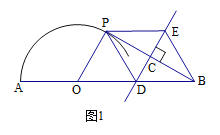
查看答案和解析>>【题目】如图,点O在线段AB上,(不与端点A、B重合),以点O为圆心,OA的长为半径画弧,线段BP与这条弧相切与点P,直线CD垂直平分PB,交PB于点C,交AB于点D,在射线DC上截取DE,使DE=DB。已知AB=6,设OA=r。
(1)求证:OP∥ED;
(2)当∠ABP=30°时,求扇形AOP的面积,并证明四边形PDBE是菱形;
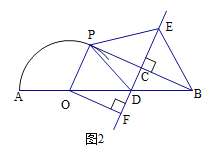
(3)过点O作OF⊥DE于点F,如图所示,线段EF的长度是否随r的变化而变化?若不变,直接写出EF的值;若变化,直接写出EF与r的关系。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(5,3),点B(-3,3),过点A的直线
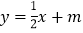 (m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D。
(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D。(1)求点P的坐标;
(2)求直线BP的解析式,并直接写出△PCD与△PAB的面积比;
(3)若反比例函数
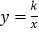 (k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值。
(k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值。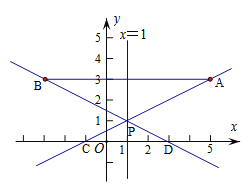
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经销一种商品,已知其每件进价为40元。现在每件售价为70元,每星期可卖出500件。该商场通过市场调查发现:若每件涨价1元,则每星期少卖出10件;若每件降价1元,则每星期多卖出m(m为正整数)件。设调查价格后每星期的销售利润为W元。
(1)设该商品每件涨价x(x为正整数)元,
①若x=5,则每星期可卖出____件,每星期的销售利润为_____元;
②当x为何值时,W最大,W的最大值是多少。
(2)设该商品每件降价y(y为正整数)元,
①写出W与Y的函数关系式,并通过计算判断:当m=10时每星期销售利润能否达到(1)中W的最大值;
②若使y=10时,每星期的销售利润W最大,直接写出W的最大值为_____。
(3)若每件降价5元时的每星期销售利润,不低于每件涨价15元时的每星期销售利润,求m的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为⊙O的内接三角形,BC=24 ,
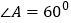 ,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )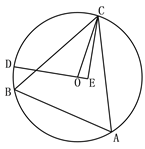
A.
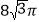 B.
B. 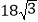 C.
C. 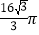 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D为AB边上一点,E为CD中点,AC=
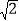 ,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
A.
 B.
B. 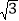 +1﹣
+1﹣ C.
C. 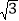 ﹣
﹣ D.
D.  ﹣1
﹣1
相关试题

