【题目】已知关于x的方程x2+ax+b=0(b≠0)与x2+cx+d=0都有实数根,若这两个方程有且只有一个公共根,且ab=cd,则称它们互为“同根轮换方程”.如x2-x-6=0与x2-2x-3=0互为“同根轮换方程”.
(1)若关于x的方程x2+4x+m=0与x2-6x+n=0互为“同根轮换方程”,求m的值;
(2)已知方程①:x2+ax+b=0和方程②:x2+2ax+![]() b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
参考答案:
【答案】(1)![]() ;(2)能,①
;(2)能,①![]() ,
,![]() ②
②![]() ,
,![]() ③
③![]() ,
,![]()
【解析】试题分析:(1)根据方程x2+4x+m=0与x2-6x+n=0互为“同根轮换方程”,得到m、n之间的关系为4m=-6n.然后设t是公共根,则有t2+4t+m=0,t2-6t+n=0,于是得到结论;(2)根据x2-x-6=0与x2-2x-3=0互为“同根轮换方程”,得到它们的公共根是3,从而得到当p=q=-3a时,有9a2-3a2+b=0.解得,b=-6a2.解得,p=-3a,x1=2a;q=-3a,x2=a,从而证得方程x2+ax+b=0(b≠0)与x2+2ax+![]() b=0互为“同根轮换方程”.
b=0互为“同根轮换方程”.
试题解析:(1)∵方程x2+4x+m=0与x26x+n=0互为“同根轮换方程”,
∴4m=6n.
设t是公共根,则有t2+4t+m=0,t26t+n=0.
解得,t=![]() .
.
∵4m=6n.∴t=![]() .
.
∴(![]() )2+4(
)2+4(![]() )+m=0.
)+m=0.
∴m=12.
(2)∵x2x6=0与x22x3=0互为“同根轮换方程”,
它们的公共根是3.
而3=(3)×(1)=3×(1).
又∵x2+x6=0与x2+2x3=0互为“同根轮换方程”。
它们的公共根是3.
而3=3×1.
∴当p=q=3a时,
有9a23a2+b=0.
解得:b=6a2.
∴x2+ax6a2=0,x2+2ax3a2=0.
解得:p=3a,x1=2a,q=3a,x2=a.
∵b≠0,
∴6a2≠0,
∴a≠0.
∴2a≠a.即x1≠x2.
又∵2a×![]() b=ab,
b=ab,
∴方程x2+ax+b=0(b≠0)与x2+2ax+12b=0能为“同根轮换方程”,p=q=3a.
-
科目: 来源: 题型:
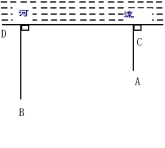
查看答案和解析>>【题目】如图,草原上,一牧童在A处放马,牧童家在B处,A、B处距河岸的距离AC,BD的长分别为500m和700m,且CD=500m,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,牧童将马牵到河边什么地方饮水,才能使走过的路程最短?牧童最少要走多少m?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若四边形的两条对角线相等,则顺次连接该四边形各边中点所得的四边形是( )
A.梯形
B.矩形
C.菱形
D.正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3x24x2=12x2B.x3+x5=x8
C.x4÷x=x3D.(x5)2=x7
-
科目: 来源: 题型:
查看答案和解析>>【题目】由四舍五入法得到的近似数10.560精确到位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克)
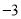
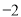

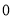
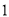
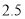
筐 数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐重______千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价
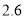 元,则出售这20筐白菜可卖多少元?
元,则出售这20筐白菜可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】下表给出了某班6名同学的身高情况(单位:cm).
学生
A
B
C
D
E
F
身高(单位:cm)
165
____
166
____
____
172
身高与班级平
均身高的差值)
-1
+2
____
-3
+4
____
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6名同学身高的达标率是多少?
相关试题

