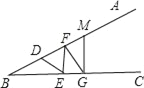
【题目】已知:如图,BD=DE=EF=FG.
(1)若∠ABC=20°,∠ABC内符合条件BD=DE=EF=FG的折线(如DE、EF、FG)共有几条?若∠ABC=10°呢?试一试,并简述理由.
(2)若∠ABC=m°(0<m<90),你能找出一个折线条数n与m之间的关系吗?若有,请找出来;若无,请说明理由.
参考答案:
【答案】(1)有4条,若∠ABC=10°,有8条;(2)n<![]() 的整数.
的整数.
【解析】
(1)根据已知可得到几组相等的角,再根据三角形外角的性质可得到∠EDF、∠FEG、∠AFG、∠AMG分别与∠B的关系,再根据三角形内角和定理即可求解.
(2)结合第(1)题,根据三角形内角和定理可知,需满足mn<90°,从而不难求解.
(1)有4条,若∠ABC=10°,有8条.
当∠ABC=20°,
∵BD=DE=EF=FG=GM,
∴∠DEB=∠B,∠EDF=∠EFD,∠FEG=∠FGE,∠GFM=∠FMG
∵∠EDF=2∠B=40°,∠FEG=3∠B=60°,∠AFG=4∠B=80°,∠AMG=5∠B=100°,
∴同理:∠AMG将成为下一个等腰三角形的底角
∵100°+100°>180°
∴不会再由下一条折线
∴共有四条拆线,分别是:DE、EF、FG,GM.
同理:当∠ABC=10°,有8条符合条件的折线.
(2)由(1)可知∠EDF=2∠B=2m°,∠FEG=3∠B=3m°,∠AFG=4∠B=4m°,
∵根据三角形内角和定理可知,需满足mn<90°,
∴n<![]() 的整数.
的整数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DE;③∠BDE=2∠BCE.其中正确结论的个数为( )

A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
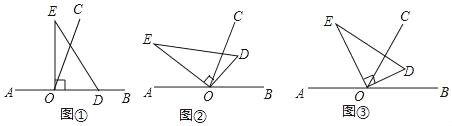
查看答案和解析>>【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为(2x+y﹣3,x﹣2y),它关于x轴的对称点A1的坐标为(x+3,y﹣4),关于y轴的对称点为A2.
(1)求A1、A2的坐标;
(2)证明:O为线段A1A2的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOC为直角,OC是∠BOD的平分线,且∠AOB=57.65°,则∠AOD的度数是( )

A. 122°20′ B. 122°21′ C. 122°22′ D. 122°23′
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.

(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
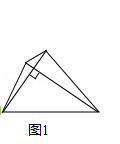
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.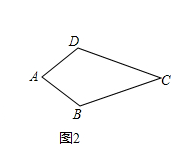
(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证).
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.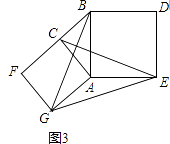
相关试题

