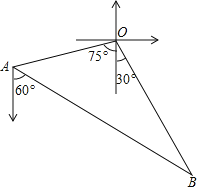
【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时15海里的速度航行,甲沿南偏西75°方向以每小时15![]() 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?
参考答案:
【答案】(15+15![]() )海里/小时
)海里/小时
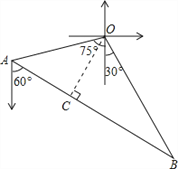
【解析】试题分析:根据题意画图,过O向AB作垂线,根据特殊角的三角函数值求得AC、BC的值,从而求得AB的值.根据追及问题的求法求甲船追赶乙船的速度;
试题解析:
解:过O作OC⊥AB于C.
则∠OAC=180°﹣60°﹣75°=45°,
可知AO=15![]() (海里),
(海里),
∴OC=AC=15![]() ×
×![]() =15(海里),
=15(海里),
∵∠B=90°﹣30°﹣30°=30°,
∴![]() =tan30°,
=tan30°,
∴![]() ,
,
∴BC=15![]() (海里),
(海里),
OB=15×2=30(海里),
乙船从O点到B点所需时间为2小时,
甲船追赶乙船速度为(15+15![]() )海里/小时.
)海里/小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一个多项式化成几个________的_______的形式,叫做把这个多项式分解因式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,长方形的两边长分别为m+1,m+7;如图②,长方形的两边
长分别为m+2,m+4.(其中m为正整数)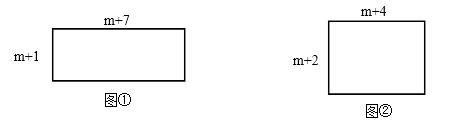
(1)图①中长方形的面积 =
=
图②中长方形的面积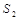 =
=
比较:
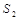 (填“<”、“=”或“>”)
(填“<”、“=”或“>”)
(2)现有一正方形,其周长与图①中的长方形周长相等,则
①求正方形的边长(用含m的代数式表示);
②试探究:该正方形面积 与图①中长方形面积
与图①中长方形面积  的差(即
的差(即  -
-  )是一个常数,求出这个常数.
)是一个常数,求出这个常数.
(3)在(1)的条件下,若某个图形的面积介于 、
、 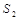 之间(不包括
之间(不包括  、
、 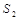 )并且面积为整数,这样的整数值有且只有10个,求m的值.
)并且面积为整数,这样的整数值有且只有10个,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)计算:(﹣2016)0+( )﹣2+(﹣3)3;
)﹣2+(﹣3)3;
(2)简算:982 -97×99. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(a,5)关于原点对称的点的坐标是(1,b+1),则点(a,b)在第象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一张边长是10cm的正方形铁皮围成一个圆柱体,这个圆柱的侧面积是__________cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(3x+9)(6x+8)= .
相关试题

