【题目】如图,在平面直角坐标系xOy中,A(m+1,0)、B(0,m)(m>0),以AB为直径画圆⊙P,点C为⊙P上一动点,
(1)判断坐标原点O是否在⊙P上,并说明理由;
(2)若点C在第一象限,过点C作CD⊥y轴,垂足为D,连接BC、AC,且∠BCD=∠BAC,
①求证:CD与⊙P相切;
②当m=3时,求线段BC的长;
(3)若点C是![]() 的中点,试问随着m的变化点C的坐标是否发生变化,若不变,求出点C的坐标;若变化,请说明理由.
的中点,试问随着m的变化点C的坐标是否发生变化,若不变,求出点C的坐标;若变化,请说明理由.

参考答案:
【答案】(1)在,理由见解析;(2)①证明见解析,②BC= ![]() ;(3)不变,C
;(3)不变,C ![]()
【解析】试题分析:(1)点P在⊙P上.连接OP.证明OP=PA,则可得到结论;
(2)①连接PC.证明∠BCD+∠PCB=90°即可得到结论;
②延长CP交OA于M.当m=3时,得到OB=3,OA=4, AB=5.再证明四边形DOMC是矩形,得到CM=DO,由三角形中位线定理得到PM=1.5,从而得到CM=4,进而得到BD=1. 再由sin∠BCD=sin∠BAC,可得到BC的长.
(3)过点C作CM⊥x轴于点M,CN⊥y轴于点N,可证明△BNC≌△AMC,设CM=a,则有ON=OM=a,故m+a=m+1-a,解出a的值即可.
试题解析:解:(1)点P在⊙P上.理由如下;
连接OP.∵BA为⊙P的直径,∴BP=PA,∵∠AOB=90°,∴OP=![]() AB=PA,∴点O在⊙P上;
AB=PA,∴点O在⊙P上;
(2)①连接PC.∵PC=PA,∴∠PCA=∠PAC,∵∠BCD=∠BAC,∴∠BCD=∠PCA.∵AB为直径,∴∠BCA=90°,∴∠BCP+∠ACP=90°,∴∠BCD+∠PCB=90°,∴CD与⊙P相切;
②延长CP交OA于M.当m=3时,OB=3,OA=4,∴AB=5.∵∠PCD=∠CDO=∠DOA=90°,∴四边形DOMC是矩形,∴CM=DO,PM⊥OA,∴OM=MA,∵AP=BP,∴PM=![]() BO=1.5,∵PC=2.5,∴CM=1.5+2.5=4,∴OD=4,∴BD=4-3=1. ∵∠BCD=∠BAC,∴sin∠BCD=sin∠BAC,∴
BO=1.5,∵PC=2.5,∴CM=1.5+2.5=4,∴OD=4,∴BD=4-3=1. ∵∠BCD=∠BAC,∴sin∠BCD=sin∠BAC,∴![]() ,∴
,∴![]() ,∴
,∴ ![]() ,∴BC=
,∴BC=![]() .
.

(3)过点C作CM⊥x轴于点M,CN⊥y轴于点N,∵弧CB=弧AC,∴BC=AC,在△BNC和△AMC中,∵∠CBN=∠MAC,∠AMC=∠BNC,BC=AC,∴△BNC≌△AMC,∴BN=AM ,CM=CN,设CM=a,∵四边形ONCM为正方形,∴ON=OM=a,∴m+a=m+1-a,解得a=![]() ,所以C(
,所以C(![]() ,
, ![]() ).∴C的坐标不变,为C(
).∴C的坐标不变,为C(![]() ,
, ![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】将从1开始的连续自然数按一下规律排列:
第1行
1
第2行
2
3
4
第3行
9
8
7
6
5
第4行
10
11
12
13
14
15
16
第5行
25
24
23
22
21
20
19
18
17
…
则2017在第行. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC,垂足为D.
(1)求证:BE=CF;
(2)若AB=8,AC=6,AD=5,求⊙O的半径.
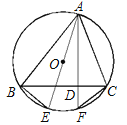
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列4个命题:①相等的角是对顶角;②互补的两个角中一定是一个为锐角,另一个为钝角;③平行于同一条直线的两条直线平行;④同位角相等.其中真命题的个数为( )
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣1)2的正确结果是( )
A.1
B.2
C.﹣1
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查某小区居民的用水情况,随机抽查了若干户家庭的月用水量,结果如下表:
月用水量(吨)
3
4
5
8
户 数
2
3
4
1
则关于这若干户家庭的月用水量,下列说法错误的是( )
A. 众数是4 B. 平均数是4.6
C. 调查了10户家庭的月用水量 D. 中位数是4.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家电销售商店1-6周销售甲、乙两种品牌冰箱的数量如图所示(单位:台):
(1)分别求该商店这段时间内甲、乙两种品牌冰箱周销售量的平均数和方差;
(2)根据计算结果及折线统计图,对该商店今后采购这两种品牌冰箱的意向提出建议,并说明理由.

相关试题

