搜索
【题目】在△ABC中，AB＝AC，AB的垂直平分线交AB于点D，交直线AC于点E，∠AEB＝80°，那么∠EBC等于（ ）
A. 15° B. 25° C. 15°或75° D. 25°或85°
参考答案：
【答案】C
【解析】
分两种情况：∠BAC为锐角，∠BAC为钝角，根据线段垂直平分线的性质可求出AE＝BE，然后根据三角形内角和定理即可解答．
如图1．
∵DE 垂直平分AB，∴AE＝BE，∴∠BAC＝∠ABE．
∵∠AEB＝80°，∴∠BAC＝∠ABE＝50°．
∵AB＝AC，∴∠ABC
65°，∴∠EBC＝∠ABC﹣∠ABE＝15°．
如图2．
∵DE 垂直平分AB，∴AE＝BE，∴∠BAE＝∠ABE．
∵∠AEB＝80°，∴∠BAE＝∠EBA＝50°，∴∠BAC＝130°．
∵AB＝AC，∴∠ABC
25°，∴∠EBC＝∠EBA+∠ABC＝75°．
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）（5mn2﹣4m2n）（﹣2mn）
（2）（x+7）（x﹣6）﹣（x﹣2）（x+1）
（3） (－
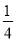)2 016×161 008；【答案】（1）﹣10m2n3+8m3n2；（2）2x﹣40；(3)1．
【解析】试题分析：（1）原式利用单项式乘以多项式法则计算即可得到结果；
（2）原式两项利用多项式乘以多项式法则计算，去括号合并即可得到结果；
（3）先根据幂的乘方的逆运算，把(－
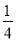)2 016化为(
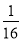)1008，再根据积的乘方的逆运算计算即可.试题解析：（1）原式=（5mn2）（﹣2mn）+（﹣4m2n）（﹣2mn）=﹣10m2n3+8m3n2；
（2）原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40．
（3）原式=(
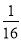)1008×161 008=(
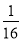×16)1 008=1.【题型】解答题
【结束】
19【题目】如图，方格图中每个小正方形的边长为1，点A、B、C都是格点．
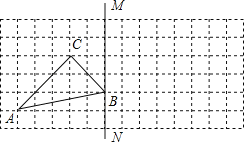
（1）画出△ABC关于直线BM对称的△A1B1C1；
（2）写出AA1的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】烟台享有“苹果之乡”的美誉．甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果．甲超市销售方案是：将苹果按大小分类包装销售，其中大苹果400千克，以进价的2倍价格销售，剩下的小苹果以高于进价10%销售．乙超市的销售方案是：不将苹果按大小分类，直接包装销售，价格按甲超市大、小两种苹果售价的平均数定价．若两超市将苹果全部售完，其中甲超市获利2100元（其它成本不计）．问：
（1）苹果进价为每千克多少元？
（2）乙超市获利多少元？并比较哪种销售方式更合算． -
科目： 来源： 题型：
查看答案和解析>>【题目】综合题。
（1）如图1，已知∠ACB=∠DCE=90°，AC=BC=6，CD=CE，AE=3，∠CAE=45°，求AD的长．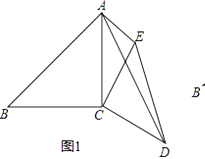
（2）如图2，已知∠ACB=∠DCE=90°，∠ABC=∠CED=∠CAE=30°，AC=3，AE=8，求AD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：等腰△ABC的底边BC长为6，面积是18，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（ ）
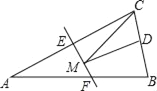
A. 6 B. 8 C. 9 D. 10
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，点P是直角三角形ABC斜边AB上一动点（不与A，B重合），分别过点A，B向直线CP作垂线，垂足分别为E，F，Q为斜边AB的中点．
（1）当点P与点Q重合时，如图1，写出QE与QF的数量关系，不证明；
（2）当点P在线段AB上且不与点Q重合时，如图2，（1）的结论是否成立？并证明；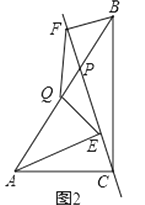
（3）当点P在线段BA（或AB）的延长线上时，如图3，此时（1）的结论是否成立？请画出图形并给予证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如下图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO＝
a°，则下列结论: ①∠BOE＝
（180-a）°；②OF平分∠BOD；③∠POE＝∠BOF；④∠POB＝2∠DOF．其中正确的个数有（ ）个．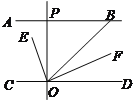
A. 1 B. 2 C. 3 D. 4
相关试题
