【题目】问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.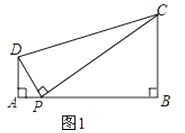
(1)求证:ADBC=APBP.
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.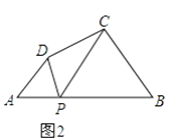
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.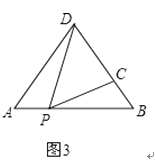
参考答案:
【答案】
(1)证明:如图1,
∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠APD=∠BPC,
∴△ADP∽△BPC,
∴ ![]() ,
,
∴ADBC=APBP
(2)结论ADBC=APBP仍成立;
理由:证明:如图2,∵∠BPD=∠DPC+∠BPC,
又∵∠BPD=∠A+∠APD,
∴∠DPC+∠BPC=∠A+∠APD,
∵∠DPC=∠A=θ,
∴∠BPC=∠APD,
又∵∠A=∠B=θ,
∴△ADP∽△BPC,
∴ ![]() ,
,
∴ADBC=APBP;
(3)解:如下图,过点D作DE⊥AB于点E,
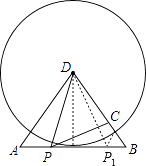
∵AD=BD=10,AB=12,
∴AE=BE=6
∴DE= ![]() =8,
=8,
∵以D为圆心,以DC为半径的圆与AB相切,
∴DC=DE=8,
∴BC=10﹣8=2,
∵AD=BD,
∴∠A=∠B,
又∵∠DPC=∠A,
∴∠DPC=∠A=∠B,
由(1)(2)的经验得ADBC=APBP,
又∵AP=t,BP=12﹣t,
∴t(12﹣t)=10×2,
∴t=2或t=10,
∴t的值为2秒或10秒
【解析】(1)要证ADBC=APBP,将等积式转化为比列式,可知需证△ADP∽△BPC,根据已知易证证明∠APD=∠BPC,即可得出结论。
(2)此题需证△ADP∽△BPC,还差一个条件,根据三角形外角性质得出∠BPD=∠DPC+∠BPC,∠BPD=∠A+∠APD,结合已知得出∠BPC=∠APD,即可证得结论。
(3)抓住已知AD=BD,过点D作DE⊥AB于点E,根据等腰三角形的性质及勾股定理求出DE的长,再以D为圆心,以DC为半径的圆与AB相切,得出DC=DE=8,从而求出BC的长,再证明∠DPC=∠A=∠B,根据前两题的证明过程可知ADBC=APBP,建立方程求出t的值。
【考点精析】根据题目的已知条件,利用因式分解法和三角形的外角的相关知识可以得到问题的答案,需要掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).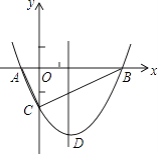
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s
150
300
600
900
1200
1500
摸到白球的频数n
63
a
247
365
484
606
摸到白球的频率
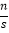
0.420
0.410
0.412
0.406
0.403
b
(1) 按表格数据格式,表中的
 = ;
= ;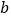 = ;
= ;(2) 请估计:当次数s很大时,摸到白球的频率将会接近 (精确到0.1);
(3)请推算:摸到红球的概率是 (精确到0.1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 E,F 是ABCD 对角线上两点,在条件①DE=BF;②∠ADE=∠CBF; ③AF=CE;④∠AEB=∠CFD 中,添加一个条件,使四边形 DEBF 是平行四边形,可添加 的条件是( )
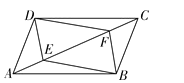
A. ①②③ B. ①②④ C. ①③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为
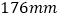 ~
~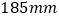 的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:收集数据(单位:
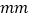 ):
):甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
组别频数
165.5~170.5
170.5~175.5
175.5~180.5
180.5~185.5
185.5~190.5
190.5~195.5
甲车间
2
4
5
6
2
1
乙车间
1
2
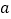
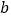
2
0
分析数据:
车间
平均数
众数
中位数
方差
甲车间
180
185
180
43.1
乙车间
180
180
180
22.6
应用数据;
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息.请判断哪个车间生产的新产品更好.并说明理由.
-
科目: 来源: 题型:
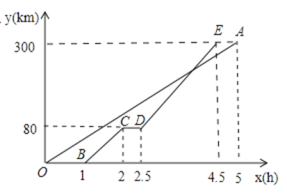
查看答案和解析>>【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发驶向乙地。如图,线段OA表示货车离甲地的距离
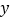 (km)与时间
(km)与时间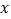 (h)之间的函数关系,折线BCDE变式轿车离甲地的距离
(h)之间的函数关系,折线BCDE变式轿车离甲地的距离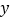 (km)与时间
(km)与时间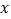 (h)之间的函数关系。根据图像,解答下列问题:
(h)之间的函数关系。根据图像,解答下列问题:(1)线段CD表示轿车在途中停留了 h.
(2)求线段DE对应的函数关系式(2.5≤x≤4.5).
(3)求轿车从甲地出发后经过多长时间追上货车.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ABC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
相关试题

