【题目】如图，在平面直角坐标系中，点A、C的坐标分别为（﹣1，0）、（0，﹣ ），点B在x轴上．已知某二次函数的图象经过A、B、C三点，且它的对称轴为直线x=1，点P为直线BC下方的二次函数图象上的一个动点（点P与B、C不重合），过点P作y轴的平行线交BC于点F．

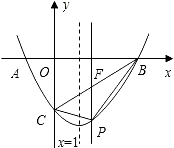
（1）求该二次函数的解析式；
（2）若设点P的横坐标为m，用含m的代数式表示线段PF的长；
（3）求△PBC面积的最大值，并求此时点P的坐标．

参考答案：

【答案】
（1）

解：设二次函数的解析式为y=ax2+bx+c（a≠0，a、b、c为常数），

由抛物线的对称性知B点坐标为（3，0），

依题意得： ，

解得： ，

∴所求二次函数的解析式为


（2）

解：∵P点的横坐标为m，

∴P点的纵坐标为 ，

设直线BC的解析式为y=kx+b（k≠0，k、b是常数），

依题意，得 ，

∴ ，

故直线BC的解析式为 ，

∴点F的坐标为 ，

∴


（3）

解：∵△PBC的面积 ，

∴当 时，△PBC的最大面积为 ，

把 代入 ，

得 ，

∴点P的坐标为


【解析】此题文字比较多，而且图象也比较复杂，所以解题时需要理解题意．（1）可以采用待定系数法求二次函数的解析式，因为点A（﹣1，0）、C（0，﹣ ）在函数图象上，对称轴为x=1，也可求得A的对称点B的坐标为（3，0），列方程组即可求得解析式；（2）先求得直线BC的解析式为 ，则可求得点F的坐标为 ，再求得点P的纵坐标为 ，可得线段PF的长；（3）利用面积和，△PBC的面积 即可求得．
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案，需要熟知二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．

关闭