搜索
【题目】列式并计算
（1）求+1.2的相反数与﹣1.3的绝对值的和．
（2）4
与2
的和的相反数．
（3）巴黎和北京的时差是﹣7个小时，李伯伯于北京时间9月29号早上8：00搭乘飞往巴黎，飞行时间约11个小时，则李伯伯到达巴黎的时间是 ．（填月日时）
参考答案：
【答案】（1）﹣（+1.2）+|﹣1.3|=0.1；（2）﹣（4
+2
）=﹣7；（3）9月29日12：00．
【解析】
（1）根据相反数和绝对值定义列出算式，再根据法则计算可得；
（2）根据题意列出算式，再由有理数的运算法则即可得；
（3）由巴黎与北京的时差为﹣7h，根据题意列出算式，计算即可得到结果．
（1）﹣（+1.2）+|﹣1.3|=﹣1.2+1.3=0.1；
（2）﹣（4+2）=﹣7；
（3）根据题意得：8+11﹣7=12，则到达巴黎得时间是12：00．
故答案为：9月29日12：00．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列推理过程，将空白部分补充完整．
（1）如图1，∠ABC=∠A1B1C1，BD，B1D1分别是∠ABC，∠A1B1C1的角平分线，对∠DBC=∠D1B1C1进行说理．
理由：因为BD，B1D1分别是∠ABC，∠A1B1C1的角平分线
所以∠DBC= ，∠D1B1C1= （角平分线的定义）
又因为∠ABC=∠A1B1C1
所以
∠ABC=∠A1B1C1所以∠DBC=∠D1B1C1（ ）
（2）如图2，EF∥AD，∠1=∠2，∠B=40°，求∠CDG的度数．
因为EF∥AD，
所以∠2= （ ）
又因为∠1=∠2 （已知）
所以∠1= （等量代换）
所以AB∥GD（ ）
所以∠B= （ ）
因为∠B=40°（已知）
所以∠CDG= （等量代换）
（3）下面是“积的乘方的法则“的推导过程，在括号里写出每一步的依据．
因为（ab）n=
（ ）=
（ ）=anbn（ ）
所以（ab）n=anbn．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，点B、C分别在边AD、AF上，此时BD=CF，BD⊥CF成立．
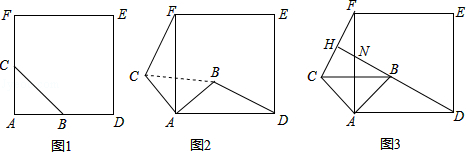
（1）当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明，若不成立，请说明理由；
（2）当△ABC绕点A逆时针旋转45°时，如图3，延长BD交CF于点H．
①求证：BD⊥CF；
②当AB=2，AD=3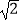
时，求线段DH的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数：
﹣3.1，3.1415，﹣
，+31，0.618，﹣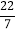
，0，﹣1，﹣（﹣3），填在相应的集合里分数集合： ；
整数集合： ；
非负整数集合： ；
正有理数集合： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将长方形纸片按如图所示的方式折叠，BC、BD为折痕．若∠ABC=25°，则∠DBE的度数为（ ）
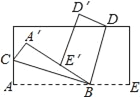
A. 50° B. 65° C. 45° D. 60°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．
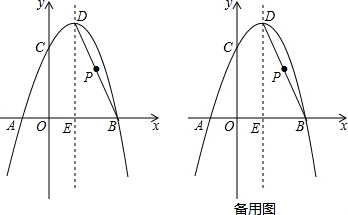
（1）求经过A，B，C三点的抛物线的函数表达式；
（2）点P是线段BD上一点，当PE=PC时，求点P的坐标；
（3）在（2）的条件下，过点P作PF⊥x轴于点F，G为抛物线上一动点，M为x轴上一动点，N为直线PF上一动点，当以F、M、N、G为顶点的四边形是正方形时，请求出点M的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】将一块长为a米，宽为b米的矩形空地建成一个矩形花园，要求在花园中修两条入口宽均为x米的小道，其中一条小道两边分别经过矩形一组对角顶点，剩余的地方种植花草，现有从左至右三种设计方案如图所示，种植花草的面积分别为S1，S2和S3，则它们的大小关系为（ ）
A. S3＜S1＜S2 B. S1＜S2＜S3 C. S2＜S1＜S3 D. S1=S2=S3
相关试题
