搜索
【题目】如图，在
中，
，过点
的直线
，
为
边上一点，过点作
交直线
于点
，垂足为点
，连结
、
．
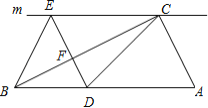
（1）求证：
；
（2）当点是中点时，四边形
是什么特殊四边形？说明你的理由；
（3）若点是中点，当四边形是正方形时，则
大小满足什么条件？
参考答案：
【答案】（1）见解析 （2）见解析 （3）
【解析】
（1）连接
，利用同角的余角相等，得到
，利用平行四边形的判定和性质得结论；
（2）先证明四边形
是平行四边形，再利用直角三角形斜边的中线等于斜边的一半说明邻边相等，证明该四边形是菱形；
（3）由平行线的性质得出
，由正方形的性质得出
，
，即可得出结论．
解：（1）证明：
，
，
，
，
，
，
，
，
四边形
是平行四边形，
；
（2）解：四边形是菱形．理由如下：
由（1）知：四边形是平行四边形，
，
，
在
中，点
是
的中点，
，
又
，
，
四边形是平行四边形，
，
四边形是菱形．
（3）解：，理由如下：
，
，
四边形是正方形，
，，
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】推理填空：
如图，已知∠1＝∠2，∠B＝∠C，可推得AB∥CD．理由如下：
∵∠1＝∠2（已知），且∠1＝∠4（ ）
∴∠2＝∠4 （等量代换）
∴CE∥BF （ ）
∴∠ ＝∠3（ ）
又∵∠B＝∠C（已知），∴∠3＝∠B（等量代换）
∴AB∥CD （ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
如图1，在平面直角坐标系xOy中，直线y1=ax+b与双曲线y2=
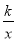交于A（1，3）和B（﹣3，﹣1）两点．观察图象可知：
①当x=﹣3或1时，y1=y2；
②当﹣3＜x＜0或x＞1时，y1＞y2，即通过观察函数的图象，可以得到不等式ax+b＞
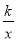的解集．有这样一个问题：求不等式x3+4x2﹣x﹣4＞0的解集．
某同学根据学习以上知识的经验，对求不等式x3+4x2﹣x﹣4＞0的解集进行了探究．
下面是他的探究过程，请将（2）、（3）、（4）补充完整：
（1）将不等式按条件进行转化：
当x=0时，原不等式不成立；
当x＞0时，原不等式可以转化为x2+4x﹣1＞
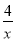；当x＜0时，原不等式可以转化为x2+4x﹣1＜
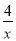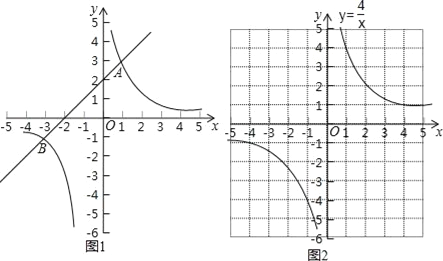
；（2）构造函数，画出图象
设y3=x2+4x﹣1，y4=
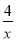，在同一坐标系中分别画出这两个函数的图象．双曲线y4=
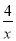如图2所示，请在此坐标系中画出抛物线y3=x2+4x﹣1；（不用列表）（3）确定两个函数图象公共点的横坐标
观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足y3=y4的所有x的值为 ；
（4）借助图象，写出解集
结合（1）的讨论结果，观察两个函数的图象可知：不等式x3+4x2﹣x﹣4＞0的解集为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在下面直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式
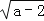+（b﹣3）2=0，（c﹣4）2≤0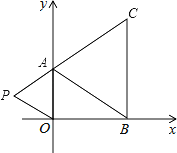
（1）求a、b、c的值；
（2）如果在第二象限内有一点P（﹣m，
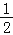），请用含m的式子表示四边形ABOP的面积；（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程2
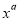-3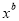
-5=0，试写出满足要求的所有a，b的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，直线y=2x+3与直线y=﹣2x﹣1.
（1）求两直线与y轴交点A，B的坐标；
（2）求两直线交点C的坐标；
（3）求△ABC的面积．
-
科目： 来源： 题型：
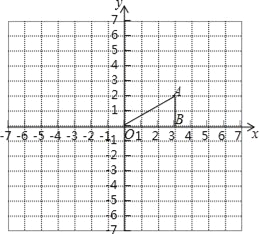
查看答案和解析>>【题目】如图，点A的坐标为（3，2），点B的坐标为（3，0）．作如下操作：
（1）以点A为旋转中心，将△ABO顺时针方向旋转90°，得到△AB1O1；
（2）以点O为位似中心，将△ABO放大，得到△A2B2O，使位似比为1：2，且点A2在第三象限．
①在图中画出△AB1O1和△A2B2O；
②请直接写出点A2的坐标： ．
③如果△ABO内部一点M的坐标为（m，n），写出点M在△A2B2O内的对应点N的坐标： ．
相关试题
