【题目】为了解某个某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温![]() (单位:
(单位:![]() )进行调查,并将所得的数据按照
)进行调查,并将所得的数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五组,得到如图频率分布直方图.
分成五组,得到如图频率分布直方图.

(1)求这30天最高气温的平均数和中位数(各组的实际数据用该组的组中值代表);
(2)每月按30天计算,各组的实际数据用该组的组中值代表,估计该地这个季度中最高气温超过(1)中平均数的天数;
(3)如果从最高气温不低于![]() 的两组内随机选取两天,请你直接写出这两天都在气温最高一组内的概率.
的两组内随机选取两天,请你直接写出这两天都在气温最高一组内的概率.
参考答案:
【答案】(1)这30天最高气温的平均数为20.4℃;中位数为22℃;(2)该地这个季度中最高气温超过(1)中平均数的天数为48天;(3)这两天都在气温最高一组内的概率为![]() .
.
【解析】
试题分析:(1)根据30天的最高气温总和除以总天数,即可得到这30天最高气温的平均数,再根据第15和16个数据的位置,判断中位数;
(2)根据30天中,最高气温超过(1)中平均数的天数,即可估计这个季度中最高气温超过(1)中平均数的天数;
(3)从6天中任选2天,共有15种等可能的结果,其中两天都在气温最高一组内的情况有6种,据此可得这两天都在气温最高一组内的概率.
试题解析:(1)这30天最高气温的平均数为:![]() =20.4℃;
=20.4℃;
∵中位数落在第三组内,∴中位数为22℃;
(2)∵30天中,最高气温超过(1)中平均数的天数为16天,
∴该地这个季度中最高气温超过(1)中平均数的天数为![]() ×90=48(天);
×90=48(天);
(3)从6天中任选2天,共有15种等可能的结果,其中两天都在气温最高一组内的情况有6种,
故这两天都在气温最高一组内的概率为![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】茂名滨海新区成立以来,发展势头良好,重点项目投入已超过2000亿元,2000亿元用科学记数法表示为亿元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是 .
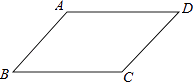
-
科目: 来源: 题型:
查看答案和解析>>【题目】若am=2,an=3,则a3m+2n=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 与
与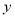 轴交于点
轴交于点 ,其顶点记为
,其顶点记为 ,自变量
,自变量 和
和 对应的函数值相等.若点
对应的函数值相等.若点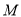 在直线
在直线 :
: 上,点
上,点 在抛物线上.
在抛物线上.(1)求该抛物线的解析式;
(2)设
 对称轴右侧
对称轴右侧 轴上方的图象上任一点为
轴上方的图象上任一点为 ,在
,在 轴上有一点
轴上有一点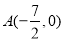 ,试比较锐角
,试比较锐角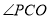 与
与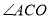 的大小(不必证明),并写出相应的
的大小(不必证明),并写出相应的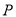 点横坐标
点横坐标 的取值范围;
的取值范围;(3)直线
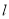 与抛物线另一点记为
与抛物线另一点记为 ,
, 为线段
为线段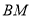 上一动点(点
上一动点(点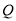 不与
不与 重合).设
重合).设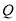 点坐标为
点坐标为 ,过
,过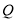 作
作
 轴于点
轴于点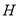 ,将以点
,将以点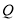 ,
, ,
, ,
, 为顶点的四边形的面积
为顶点的四边形的面积 表示为
表示为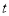 的函数,标出自变量
的函数,标出自变量 的取值范围,并求出
的取值范围,并求出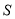 可能取得的最大值.
可能取得的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. 轴对称图形的对称点一定在对称轴的两侧
B. 两个关于某直线对称的图形一定全等
C. 两个成轴对称的图形对应点的连线的垂直平分线是它们的对称轴
D. 平面上两个全等的图形不一定关于某直线对称
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家提倡“低碳减排”,湛江某公司计划在海边建风能发电站,电站年均发电量约为213000000度,若将数据213000000用科学记数法表示为( )
A.213×106
B.21.3×107
C.2.13×108
D.2.13×109
相关试题

