【题目】如图，在Rt△ABC中，∠BAC=90°，AB=AC．

（1）利用尺规，以AB为直径作⊙O，交BC于点D；（保留作图痕迹，不写作法）

（2）在（1）所作的图形中，求证：AC2=CDCB．

参考答案：

【答案】（1）作图见解析；（2）证明见解析.

【解析】试题分析：（1）作AB的垂直平分线得到AB的中点O，然后以O为圆心，OA为半径作圆交BC于D；

（2）先利用圆周角定理得到∠ADB=∠CAB，则可判断△CAD∽△CBA，然后利用相似比得到CA：CB=CD：CA，再根据比例的性质即可得到结论．

试题解析：（1）如图所示：

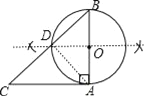
（2）连接AD，如图，

∵AB是直径，∴∠ADB=90°，∴∠ADB=∠CAB，

∵∠C=∠C，∴△CAD∽△CBA，∴CA：CB=CD：CA，

∴AC2=CDCB．

关闭