【题目】如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=AB,已知△ABE≌△ADF. 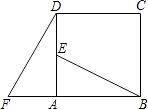
(1)在图中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置;
(2)线段BE与DF有什么关系?证明你的结论.
参考答案:
【答案】
(1)解:把△ABE绕点A逆时针旋转90°可得到△ADF
(2)解:BE=DF,BE⊥DF.理由如下:
∵△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
而∠AEB=∠DEH,
∴∠DHE=∠EAB=90°,
∴BE⊥DF.
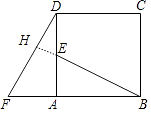
【解析】(1)利用正方形的性质得到∠BAD=90°,而△ABE≌△ADF,则利用旋转的定义可将△ABE绕点A逆时针旋转90°可得到△ADF;(2)利用全等三角形的性质可得BE=DF,ABE=∠ADF,则利用对顶角相等和三角形内角和可判断∠DHE=∠EAB=90°,从而得到BE⊥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个数中,最小的数是( )
A.﹣1
B.0
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】凯里市某文具店某种型号的计算器每只进价12元,售价20元,多买优惠,优势方法是:凡是一次买10只以上的,每多买一只,所买的全部计算器每只就降价0.1元,例如:某人买18只计算器,于是每只降价0.1×(18﹣10)=0.8(元),因此所买的18只计算器都按每只19.2元的价格购买,但是每只计算器的最低售价为16元.
(1)求一次至少购买多少只计算器,才能以最低价购买?
(2)求写出该文具店一次销售x(x>10)只时,所获利润y(元)与x(只)之间的函数关系式,并写出自变量x的取值范围;
(3)一天,甲顾客购买了46只,乙顾客购买了50只,店主发现卖46只赚的钱反而比卖50只赚的钱多,请你说明发生这一现象的原因;当10<x≤50时,为了获得最大利润,店家一次应卖多少只?这时的售价是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)25÷5×(﹣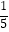 )÷(﹣
)÷(﹣  )
)
(2)( ﹣
﹣  +
+ 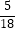 )×(﹣18)
)×(﹣18)
(3)﹣72+2×(﹣3)2+(﹣6)÷(﹣ )2
)2
(4)(﹣3)3﹣[3+0.4×(﹣1 )]÷(﹣2)
)]÷(﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2a3=a6
B.(ab)2=ab2
C.2a4×3a5=6a9
D.(a2)3=a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:9﹣p2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( ).
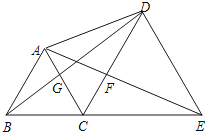
A.△ACE≌△BCD
B.△BGC≌△AFC
C.△DCG≌△ECF
D.△ADB≌△CEA
相关试题

