【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE. 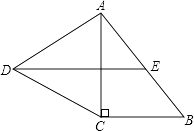
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
参考答案:
【答案】
(1)证明:连结CE.
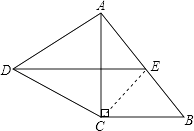
∵点E为Rt△ACB的斜边AB的中点,
∴CE= ![]() AB=AE.
AB=AE.
∵△ACD是等边三角形,
∴AD=CD.
在△ADE与△CDE中,  ,
,
∴△ADE≌△CDE(SSS),
∴∠ADE=∠CDE=30°.
∵∠DCB=150°,
∴∠EDC+∠DCB=180°.
∴DE∥CB
(2)解:当AC= ![]() 或AB=2AC时,四边形DCBE是平行四边形,
或AB=2AC时,四边形DCBE是平行四边形,
理由:∵AC= ![]() ,∠ACB=90°,
,∠ACB=90°,
∴∠B=30°,
∵∠DCB=150°,
∴∠DCB+∠B=180°,
∴DC∥BE,又∵DE∥BC,
∴四边形DCBE是平行四边形.
【解析】(1)首先连接CE,根据直角三角形的性质可得CE= ![]() AB=AE,再根据等边三角形的性质可得AD=CD,然后证明△ADE≌△CDE,进而得到∠ADE=∠CDE=30°,再有∠DCB=150°可证明DE∥CB;(2)当AC=
AB=AE,再根据等边三角形的性质可得AD=CD,然后证明△ADE≌△CDE,进而得到∠ADE=∠CDE=30°,再有∠DCB=150°可证明DE∥CB;(2)当AC= ![]() 或AB=2AC时,四边形DCBE是平行四边形.根据(1)中所求得出DC∥BE,进而得到四边形DCBE是平行四边形.
或AB=2AC时,四边形DCBE是平行四边形.根据(1)中所求得出DC∥BE,进而得到四边形DCBE是平行四边形.
-
科目: 来源: 题型:
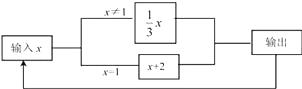
查看答案和解析>>【题目】如图是一个运算程序的示意图,若开始输入的x值为81,我们看到第一次输出的结果为27,第二次输出的结果为9,…,第2017次输出的结果为( )
A.1
B.3
C.9
D.27 -
科目: 来源: 题型:
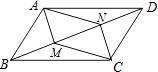
查看答案和解析>>【题目】已知:如图,在ABCD中,M、N是对角线BD上的两点,且BM=DN. 求证:四边形AMCN是平行四边形.
-
科目: 来源: 题型:
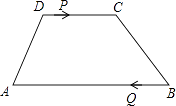
查看答案和解析>>【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣x3ya与xby是同类项,则a+b的值为( )
A.5
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程kx2+4x+1=0有两个实数根,则k的取值范围是( )
A. k>4B. k≥4C. k≤4D. k≤4且k≠0
-
科目: 来源: 题型:
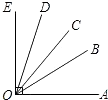
查看答案和解析>>【题目】如图所示,∠AOE=90°,∠BOD=45°,那么图中不大于90°的角有个,它们的度数之和是°.
相关试题

