【题目】如图1,已知A(![]() ,0),B(0,
,0),B(0, ![]() )分别为两坐标轴上的点,且
)分别为两坐标轴上的点,且![]() 、
、![]() 满足
满足![]() ,OC∶OA=1∶3.
,OC∶OA=1∶3.
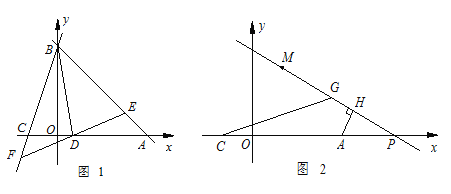
(1)求A、B、C三点的坐标;
(2)若D(1,0),过点D的直线分别交AB、BC于E、F两点,设E、F两点的横坐标分别为![]() .当BD平分△BEF的面积时,求
.当BD平分△BEF的面积时,求![]() 的值;
的值;
(3)如图2,若M(2,4),点P是![]() 轴上A点右侧一动点,AH⊥PM于点H,在HM上取点G,使HG=HA,连接CG,当点P在点A右侧运动时,∠CGM的度数是否改变?若不变,请求其值;若改变,请说明理由.
轴上A点右侧一动点,AH⊥PM于点H,在HM上取点G,使HG=HA,连接CG,当点P在点A右侧运动时,∠CGM的度数是否改变?若不变,请求其值;若改变,请说明理由.
参考答案:
【答案】(1)A(6,0),B(0,6),C(-2,0);(2)![]() ;(3)不改变.
;(3)不改变.
【解析】试题分析:(1)由偶次方和算术平方根的非负性质求出a和b的值,得出点A、B的坐标,再求出OC,即可得出点C的坐标;
(2)作EG⊥x轴于G,FH⊥x轴于H,由三角形的面积关系得出DF=DE,由AAS证明△FDH≌△EDG,得出DH=DG,即可得出结果;
(3)作MQ⊥x轴于Q,连接CM、AG、M,证出△MCQ是等腰直角三角形,得出∠MCQ=45°,同理:△MPQ是等腰直角三角形,∠MAQ=45°,△AHG是等腰直角三角形,得出∠AGH=45°=∠MCQ,证出A、G、M、C四点共圆,由圆周角定理即可得出结论.
试题解析:(1)∵![]() ,
,
∴a-b=0,b-6=0,
∴a=b=6,
∴A(6,0),B(0,6),
∴OA==OB=6,
∵OC:OA=1:3,
∴OC=2,
∴C(-2,0).
(2)作EG⊥x轴于G,FH⊥x轴于H,如图1所示:
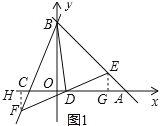
则∠FHD=∠EGD=90°,
∵BD平分△BEF的面积,
∴DF=DE,
在△FDH和△EDG中, 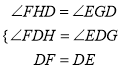 ,
,
∴△FDH≌△EDG(AAS),
∴DH=DG,即xE+1=xF1,
∴xE+xF=2;
(3)∠CGM的度数不改变,∠CGM=45°;
理由如下:作MQ⊥x轴于Q,连接CM、AG、M,如图2所示:
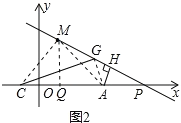
则MQ=4,OQ=2,
∴CQ=2+2=4,
∴△MCQ是等腰直角三角形,
∴∠MCQ=45°,
同理:△MQA是等腰直角三角形,
∴∠MAQ=45°,
∵AH⊥PM,HG=HA,
∴△AHG是等腰直角三角形,
∴∠AGH=45°=∠MCQ,
∴A、G、M、C四点共圆,
∴∠CGM=∠MAQ=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】16050000用科学计数法表示为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,且∠1=20°,∠2=45°+α,∠3=60°-α,∠4=40°-α,∠5=30°.则α的值为( )
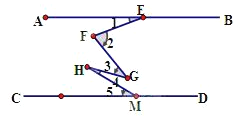
A. 10° B. 15° C. 20° D. 25°
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队合作一项工程,10天可以完成,如果单独做甲队需要的天数是乙队的两倍.
(1)求两队单独做各需多少天完成?
(2)将工程分成两部分,甲做其中一部分用了m天,乙做另一部分用了n天,其中m、n均为正整数,且m<10,n<12,直接写出m、n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年共享单车横空出世,更好地解决了人们“最后一公里”出行难的问题,截止到2016年底, “ofo共享单车”的投放数量是“摩拜单车”投放数量的1.6倍,覆盖城市也远超于“摩拜单车”, “ofo共享单车”注册用户量约为960万人,“摩拜单车”的注册用户量约为750万人,据统计使用一辆“ofo共享单车”的平均人数比使用一辆“摩拜单车”的平均人数少3人,假设注册这两种单车的用户都在使用共享单车,求2016年“摩拜单车”的投放数量约为多少万台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】0.5的相反数是( )
A.﹣0.5B.0.5C.2D.﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点B、C、E三点在同一条直线上,CD平分∠ACE,∠DBM=∠DAN,DM⊥BE于M,DN⊥AC于N.(1)求证:△BDM≌△ADN ;(2)若AC=2,BC=1,求CM的长.

相关试题

