搜索
【题目】在如图所示的运算流程中，
（1）若输入的数x=﹣4，则输出的数y= ；
（2）若输出的数y=5，则输入的数x= ．
参考答案：
【答案】（1）2.5；（2）﹣9或19.
【解析】
（1）按照运算流程计算即可；
（2）按照运算流程反推即可，注意最后输出的数可能是经过一次计算，也可能是经过多次循环计算.
解：（1）若输入x=﹣4，则﹣4﹣（﹣1）2=﹣4﹣1=﹣5，
﹣5÷（﹣2）=2.5＞0，
∴输出的数为2.5．
故答案为：2.5．
（2）若输出的数是5，则5×（﹣2）=﹣10，
﹣10+（﹣1）2=﹣10+1=﹣9．
若只经过一次流程，则输入的数是﹣9，
若-9为上一次流程计算所得结果，则，-9×（﹣2）+（﹣1）2=19，
故经过两次流程，则输入的数是19，此时不可能发生三次流程运算，
故答案为：﹣9或19．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两校的学生人数基本相同，为了解这两所学校学生的数学学业水平，在同一次测试中，从两校各随机抽取了30名学生的测试成绩进行调查分析，其中甲校已经绘制好了条形统计图，乙校只完成了一部分．
甲校 93 82 76 77 76 89 89 89 83 87 88 89 84 92 87
89 79 54 88 92 90 87 68 76 94 84 76 69 83 92
乙校 84 63 90 89 71 92 87 92 85 61 79 91 84 92 92
73 76 92 84 57 87 89 88 94 83 85 80 94 72 90
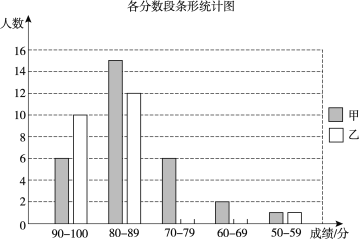
（1）请根据乙校的数据补全条形统计图；
（2）两组样本数据的平均数、中位数、众数如下表所示，请补全表格；
平均数
中位数
众数
甲校
83.4
87
89
乙校
83.2
（3）两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些，
请为他们各写出一条可以使用的理由；
甲校： ．乙校： ．
（4）综合来看，可以推断出 校学生的数学学业水平更好一些，理由为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在菱形ABCD中，CE⊥AB交AB延长线于点E，点F为点B关于CE的对称点，连接CF，分别延长DC，CF至点G，H，使FH=CG，连接AG，DH交于点P．
（1）依题意补全图1；
（2）猜想AG和DH的数量关系并证明；
（3）若∠DAB=70°，是否存在点G，使得△ADP为等边三角形？若存在，求出CG的长；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，对于与坐标轴不平行的直线l和点P，给出如下定义：过点P作x轴，y轴的垂线，分别交直线l于点M，N，若PM+PN≤4，则称P为直线l的近距点，特别地，直线上l所有的点都是直线l的近距点．已知点A(-
，0)，B(0，2)，C(-2，2)．（1）当直线l的表达式为y=x时，
①在点A，B，C中，直线l的近距点是 ；
②若以OA为边的矩形OAEF上所有的点都是直线l的近距点，求点E的纵坐标n的取值范围；
（2）当直线l的表达式为y=kx时，若点C是直线l的近距点，直接写出k的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=15，AC=20，BC边上高AD=12，则BC的长为（ ）
A. 25 B. 7 C. 25或7 D. 不能确定
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，矩形ABCD边AB=6，BC=8，再沿EF折叠，使D点与B点重合，C点的对应点为G，将△BEF绕着点B顺时针旋转，旋转角为a（0°＜a＜180°），记旋转这程中的三角形为△BE′F′，在旋转过程中设直线E′F′与射钱EF、射线ED分别交于点M、N，当EN=MN时，则FM的长为_____．
-
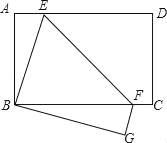
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，直线y=--
x＋8与x轴，y轴分别交于点A，点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．(1)求AB的长和点C的坐标；
(2)求直线CD的表达式．
相关试题
