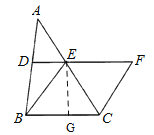
【题目】如图,在![]() 中,
中,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,延长
,延长![]() 到点F,使得
到点F,使得![]() ,连结
,连结![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,
,![]() ,求菱形
,求菱形![]() 的面积.
的面积.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】
(1)从所给的条件可知,DE是△ABC的中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=EF,所以是菱形;
(2)由∠BEF是120°,可得∠EBC为60°,即可得△BEC是等边三角形,求得BE=BC=CE=5,再过点E作EG⊥BC于点G,求出高EG的长,即可求得答案.
解:(1)∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC,
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形,
又∵BE=EF,
∴四边形BCFE是菱形;
(2)∵∠BEF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴BE=BC=CE=5,
过点E作EG⊥BC于点G,
∴EG=BEsin60°=5×![]() ,
,
∴S菱形BCFE=BCEG=5×![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.

(1)求∠EOB的度数.
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化? 若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA? 若存在,求出∠OBA的度数;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1 , △A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2 .
(1)画出△A1B1Cl和△A2B2C2;
(2)P(a,b)是△ABC的AC边上一点,△ABC经旋转、平移后点P的对应点分别为P1、P2 , 请写出点P1、P2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.

(1)猜想四边形PCOB是什么四边形,并说明理由;
(2)当矩形ABCD满足什么条件时,四边形PCOB是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x米,则可得方程
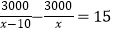 ,根据此情景,题中用“…”表示的缺失的条件应补为( )
,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期15天才完成
B.每天比原计划少铺设10米,结果延期15天才完成
C.每天比原计划多铺设10米,结果提前15天才完成
D.每天比原计划少铺设10米,结果提前15天才完成 -
科目: 来源: 题型:
查看答案和解析>>【题目】某开发区在一项工程招标时,接到甲、乙两个工程队的投标书,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:①甲队单独完成这项工程,刚好如 期完成;②乙队单独完成此项工程要比规定工期多用5天;③
 ,剩下的工程由乙队单独做,也正好如期完工.小亮设规定的工期为x天,根据题意列出了方 程:
,剩下的工程由乙队单独做,也正好如期完工.小亮设规定的工期为x天,根据题意列出了方 程:  ,则方案③中被墨水污染的部分应该是( )
,则方案③中被墨水污染的部分应该是( )
A.甲先做了4天
B.甲乙合作了4天
C.甲先做了工程的
D.甲乙合作了工程的
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠B=90°,AB=3cm,BC=4cm.点D在AC上,AD=1cm,点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了2cm,并沿B→C→A的路径匀速运动;点Q保持速度不变,并继续沿原路径匀速运动,两点在D点处再次相遇后停止运动,设点P原来的速度为xcm/s.
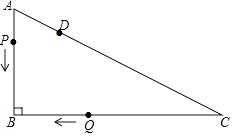
(1)点Q的速度为cm/s(用含x的代数式表示).
(2)求点P原来的速度.
相关试题

