搜索
【题目】阅读以下两小题后作出相应的解答:
（1）“同位角相等，两直线平行”，“两直线平行，同位角相等”，这两个命题的题设和结论在命题中的位置恰好对凋，我们把其中一命题叫做另一个命题的逆命题，请你写出命题“角平分线上的点到角两边的距离相等“的逆命题，并指出逆命题的题设和结论；
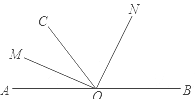
（2）根据以下语句作出图形，并写出该命题的文字叙述.已知：过直线AB上一点O任作射线OC ， OM、ON分别平分∠AOC、∠BOC ， 则OM⊥ON ．
参考答案：
【答案】
（1）逆命题是：到角两边距离相等的点在这个角的平分线上，题设是到角两边距离相等的点，结论是该点在这个角的平分线上；
（2）邻补角的平分线互相垂直
【解析】解答：（1）根据题意作出图形，由AB是一直线，即可求出∠AOB=180°，然后根据角平分线的性质，推出 
，则 
即可．（1）逆命题是：到角两边距离相等的点在这个角的平分线上，题设是到角两边距离相等的点，结论是该点在这个角的平分线上（2）如图：
该命题的文字描述是：邻补角的平分线互相垂直．
分析：对于两个命题，如果一个命题的条件和结论分别是另外一个命题的结论和条件，那么这两个命题叫做互逆命题，其中一个命题叫做原命题，另外一个命题叫做原命题的逆命题．根据定义可写出上述命题的逆命题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在梯形ABCD中，AB∥DC，过对角线AC的中点O作EF⊥AC，分别交边AB、CD于点E、F，连接CE、AF．
（1）求证：四边形AECF是菱形；
（2）若EF=4，tan∠OAE=
，求四边形AECF的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解方程：3x﹣2（x﹣1）=2﹣3（5﹣2x）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学习相似三角形时，某班举行了以“生活中的相似”为主题的测试活动，全班学生的测试成绩统计如下表：
得分（分）
85
89
93
95
100
人数（人）
4
6
13
15
2
则这些学生得分的众数是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），AB∥CD，猜想∠BPD与∠B，∠D的关系，说出理由．
解：猜想∠BPD+∠B+∠D=360°
理由：过点P作EF∥AB，
∴∠B+∠BPE=180°（两直线平行，同旁内角互补）
∵AB∥CD，EF∥AB，
∴EF∥CD，（如果两条直线都和第三条直线平行，那么这两条直线也互相平行．）
∴∠EPD+∠D=180°（两直线平行，同旁内角互补）
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
（1）依照上面的解题方法，观察图（2），已知AB∥CD，猜想图中的∠BPD与∠B，∠D的关系，并说明理由．
（2）观察图（3）和（4），已知AB∥CD，猜想图中的∠BPD与∠B，∠D的关系，不需要说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=x2﹣4x﹣4的顶点坐标为（ ）
A.（2，﹣8）
B.（2，8）
C.（﹣2，8）
D.（﹣2，﹣8） -
科目： 来源： 题型：
查看答案和解析>>【题目】义务教育均衡发展是一种新的教育发展观，是解决我国目前教育问题的新举措．其最终目标，就是要合理配置教育资源，办好每一所学校，教好每一个学生，实现教育公平．我们县级政府为推进义务教育均衡发展工作的评估，今年预算办学经费约为3亿5千万，请你用科学记数法表示应是（ ）
A.3.5×108
B.3.5×109
C.35×108
D.0.35×109
相关试题
