【题目】如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.
(1)当∠AOB=18°时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到0.01cm)
(参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科学计算器)

参考答案:
【答案】(1)3.13cm;(2)0.98cm.
【解析】
试题分析:(1)根据题意作辅助线OC⊥AB于点C,根据OA=OB=10cm,∠OCB=90°,∠AOB=18°,可以求得∠BOC的度数,从而可以求得AB的长;
(2)由题意可知,作出的圆与(1)中所作圆的大小相等,则AE=AB,然后作出相应的辅助线,画出图形,从而可以求得BE的长,本题得以解决.
试题解析:(1)作OC⊥AB于点C,如右图2所示,由题意可得,OA=OB=10cm,∠OCB=90°,∠AOB=18°,∴∠BOC=9°,∴AB=2BC=2OBsin9°≈2×10×0.1564≈3.13cm,即所作圆的半径约为3.13cm;
(2)作AD⊥OB于点D,作AE=AB,如下图3所示,∵保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,∴折断的部分为BE,∵∠AOB=18°,OA=OB,∠ODA=90°,∴∠OAB=81°,∠OAD=72°,∴∠BAD=9°,∴BE=2BD=2ABsin9°≈2×3.13×0.1564≈0.98cm,即铅笔芯折断部分的长度是0.98cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
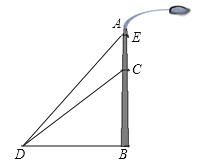
-
科目: 来源: 题型:
查看答案和解析>>【题目】在1000个数据中,用适当的方法抽取50个作为样本进行统计.在频数分布表中,54.5~57.5这一组的频率为0.12,那么这1000个数据中落在54.5~57.5之间的数据约有个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】几个不等式的解集的,叫做由它们所组成的不等式组的解集.判断不等式组解集的口诀:同大取大,同小取小,小大大小中间找,大大小小找不到.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求不等式组解集的过程,叫做.解一元一次不等式组通常采用“分开解,集中判”的方法.分开解就是分别求出不等式组中各个,并在同一数轴上表示出来;集中判是取各个不等式的解集的,即可求得不等式组的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商人在一次买卖中均以120元卖出两件衣服,一件赚25%,一件赔25%,在这次交易中,该商人( )
A.赚16元
B.赔16元
C.不赚不赔
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个相似三角形的相似比为1:4,那么它们的面积比为 .
相关试题

