【题目】在△ABC中,AC=BC,∠ACB=90°,D、E是直线AB上两点.∠DCE=45°
(1)当CE⊥AB时,点D与点A重合,求证:DE2=AD2+BE2
(2)当AB=4时,求点E到线段AC的最短距离
(3)当点D不与点A重合时,探究:DE2=AD2+BE2是否成立?若成立,请证明;若不成立,请说明理由

参考答案:
【答案】(1)证明见详解;(2)![]() ;(3)成立,证明见详解.
;(3)成立,证明见详解.
【解析】
(1)由等腰直角三角形的性质直接得出结果;
(2)当CE⊥AB时,点D与点A重合时,点E到AC的距离最短;过点E作EG⊥AC于点G,由等腰直角三角形的性质,得到AG=GE,然后利用勾股定理即可得到GE的长度;
(3)作AF⊥AB,使AF=BE,连接DF,根据SAS证得△CAF≌△CBE和△CDF≌△CDE,再由勾股定理和等量代换即可解答;
(1)解:如图:当CE⊥AB时,点D与点A重合,
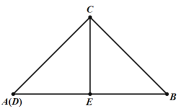
∵CE⊥AB,
∴AE=BE,
∵点D与点A重合,
∴DE=BE,
∴DE2=AD2+BE2;
(2)根据题意,当CE⊥AB时,点D与点A重合时,点E到AC的距离最短;
过点E作EG⊥AC于点G,如图:
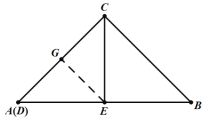
在等腰直角三角形ABC中,
∠A=45°,AE=BE=![]() ,
,
∴△AGE是等腰直角三角形,即AG=GE,
由勾股定理,得:![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴点E到线段AC的最短距离为:![]() ;
;
(3)![]() 成立;
成立;
证明:过点A作AF⊥AB,使AF=BE,连接DF,CF,
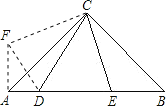
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠B=45°,
∴∠FAC=45°,
∴△CAF≌△CBE(SAS),
∴CF=CE,∠ACF=∠BCE,
∵∠ACB=90°,∠DCE=45°,
∴∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,
∵∠ACF=∠BCE,
∴∠ACD+∠ACF=45°,
即∠DCF=45°,
∴∠DCF=∠DCE,
又∵CD=CD,
∴△CDF≌△CDE(SAS),
∴DF=DE,
∵![]() ,
,
∴![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学分别用标有数字0、﹣1、4的三张卡片(除了数字不同以外,其余都相同)做游戏,他们将卡片洗匀后,将标有数字的一面朝下放在桌面上,甲先随机抽取一张,抽出的卡片放回,乙再从三张卡片中随机抽取一张.若规定甲同学抽到卡片上的数字比乙同学抽取到卡片上的数字大,则甲同学获胜;否则乙同学获胜.请你用列表法或画树状图法求哪名同学获胜的概率大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O上有一个动点A和一个定点B,令线段AB的中点是点P,过点B作⊙O的切线BQ,且BQ=3,现测得
 的长度是
的长度是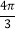 ,
,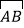 的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )
的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )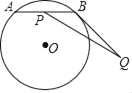
A. 3
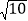 B. 2
B. 2 C. 9 D. 10
C. 9 D. 10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC 中,∠ACB=90°,AC=6,BC=8,点D是线段AB上的动点,M、N分别是AD、CD的中点,连接MN,当点D由点A向点B运动的过程中,线段MN所扫过的区域的面积为_____.
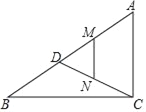
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC(AC<AB<BC),用尺规在线段BC上确定一点P,使得PA+PC=BC,则符合要求的作图痕迹是( )

A.如图① 以B为圆心,BA长为半径画弧交BC于点P
B.如图②作AC中垂线交BC于点P
C.如图③以C为圆心,CA 长为半径画弧交BC于点P
D.如图④作AB中垂线交BC于P
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
 在图中画出与
在图中画出与 关于直线l成轴对称的
关于直线l成轴对称的 ;
; 三角形ABC的面积为______;
三角形ABC的面积为______; 以AC为边作与
以AC为边作与 全等的三角形,则可作出______个三角形与
全等的三角形,则可作出______个三角形与 全等;
全等; 在直线l上找一点P,使
在直线l上找一点P,使 的长最短.
的长最短.
相关试题

