【题目】已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
参考答案:
【答案】
(1)
解答: a=20
(2)
解答:此说法不正确.
理由如下:尽管当n=3、20、120时,a>b或a<b,
但可令a=b,得 ![]() ,
,
∴60n+420=67n,
解得n=60,
经检验n=60是方程的根.
∴当n=60时,a=b,即不符合这一说法的n的值为60.
【解析】根据正多边形的每条边相等,可知边长=周长÷边数;分别表示出a和b的代数式,让其相等,看是否有相应的值.
【考点精析】本题主要考查了正多边形和圆的相关知识点,需要掌握圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(3,x+1)在第四象限,那么x的取值范围为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知3x+4≤2(3+x),则|x+1|的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(a,b)在一次函数y=4x+3的图象上,则代数式4a﹣b﹣2的值等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果若干个一元一次方程的根都是整数且是一元一次不等式组所有整数解,则称这些一元一次方程为该不等式组的紧密关联方程.如不等式组
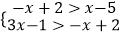 ,可以有紧密关联方程x-1=0 , x-2=0,x-3=0;(不固定),若方程3-x=2x,2x=4都是关于x的不等式组
,可以有紧密关联方程x-1=0 , x-2=0,x-3=0;(不固定),若方程3-x=2x,2x=4都是关于x的不等式组 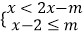 的紧密关联方程,则m的取值范围为( )
的紧密关联方程,则m的取值范围为( )
A.-1<m≤0
B.1≤m<2
C.0≤m<1
D.2<m≤3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在五边形ABCDE中,∠A+∠B+∠E=∠EDC+∠BCD+140°,DF,CF分别平分∠EDC和∠BCD,则∠F的度数为( )
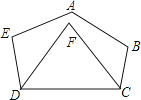
A.100°
B.90°
C.80°
D.70° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的对角线条数为( )
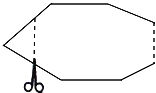
A.77
B.90
C.65
D.104
相关试题

