【题目】如图,在五边形ABCDE中,∠A+∠B+∠E=∠EDC+∠BCD+140°,DF,CF分别平分∠EDC和∠BCD,则∠F的度数为( ) 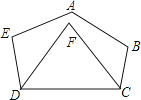
A.100°
B.90°
C.80°
D.70°
参考答案:
【答案】C
【解析】解答:∵五边形的内角和等于540°,∠A+∠B+∠E=∠EDC+∠BCD+140°,
∴2∠BCD+∠CDE=540°-140°=400°,
∵∠BCD、∠CDE的平分线在五边形内相交于点F,
∴∠FDC+∠FCD= ![]() (∠BCD+∠CDE)=100°,
(∠BCD+∠CDE)=100°,
∴∠F=80°.
分析:此题解出∠BCD+∠CDE和∠FDC+∠FCD是解题的关键;解此类题时,要求出五边形中∠BCD,∠CDE的度数,缺乏条件,即可将求∠BCD,∠CDE的度数转换求∠BCD+∠CDE的问题.
【考点精析】根据题目的已知条件,利用多边形内角与外角的相关知识可以得到问题的答案,需要掌握多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(a,b)在一次函数y=4x+3的图象上,则代数式4a﹣b﹣2的值等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果若干个一元一次方程的根都是整数且是一元一次不等式组所有整数解,则称这些一元一次方程为该不等式组的紧密关联方程.如不等式组
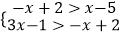 ,可以有紧密关联方程x-1=0 , x-2=0,x-3=0;(不固定),若方程3-x=2x,2x=4都是关于x的不等式组
,可以有紧密关联方程x-1=0 , x-2=0,x-3=0;(不固定),若方程3-x=2x,2x=4都是关于x的不等式组 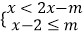 的紧密关联方程,则m的取值范围为( )
的紧密关联方程,则m的取值范围为( )
A.-1<m≤0
B.1≤m<2
C.0≤m<1
D.2<m≤3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的对角线条数为( )
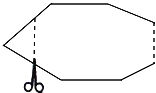
A.77
B.90
C.65
D.104 -
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
-
科目: 来源: 题型:
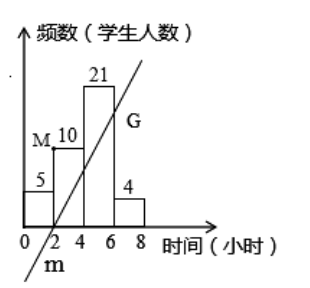
查看答案和解析>>【题目】为了了解我区某校“校园阅读”的建设情况,检查组随机抽取40名学生,调查他们一周阅读课外书籍的时间,并将结果绘成了频数分布直方图,我们把每一个直方图的时间与学生数的积看成直方图的“面积”,时间为横轴,学生人数为纵轴构成直角坐标系,规定点M的坐标为(2,10),直线m经过点(2,0)交直方图于一点G,直线m把四个直方图面积分成相等两部分,则G点坐标为.
相关试题

