【题目】![]() 年
年![]() 月,振华中学举行了迎国庆中华传统文化节活动.本次文化节共有五个活动:
月,振华中学举行了迎国庆中华传统文化节活动.本次文化节共有五个活动:![]() 书法比赛;
书法比赛;![]() 国画竞技;
国画竞技;![]() 诗歌朗诵;
诗歌朗诵;![]() 汉字大赛;
汉字大赛;![]() 古典乐器演奏.活动结束后,某班数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
古典乐器演奏.活动结束后,某班数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
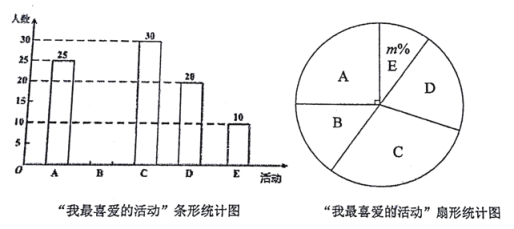
(1)此次催记抽取的初三学生共 人,![]() ,并补全条形统计图;
,并补全条形统计图;
(2)初三年级准备在五名优秀的书法比赛选手中任意选择两人参加学校的最终决赛,这五名选手中有三名男生和两名女生,用树状图或列表法求选出的两名选手正好是一男一女的概率是多少.
参考答案:
【答案】(1)100,10,图形见解析;(2)![]() .
.
【解析】
(1)根据A的人数与所占百分比即可得到抽取总人数,用选择E类的人数除以总人数求得m的值,再用总人数减去选择A、C、D、E的人数得到选择B类的学生人数,然后补全条形图即可;
(2)根据题意画出树状图,然后利用概率公式求解即可.
解:(1)根据扇形统计图可知,选A的学生所占百分比为:![]() ,
,
则抽取的学生总数为:25÷25%=100人,
选择E的学生所占百分比为:![]() ,
,
选择B的学生人数为:100﹣25﹣30﹣20﹣10=15人,
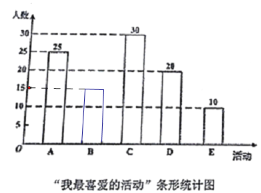
故答案为:100,10;条形图如下:
(2)树状图如下:

∵有20种可能等结果,其中符合条件的有12种,
∴选出的两名选手正好是一男一女的概率是:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请将下列事件发生的概率标在图1中(用字母表示):
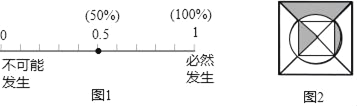
(1)记为点A:随意掷两枚质地均匀的骰子,朝上面的点数之和为1;
(2)记为点B:抛出的篮球会下落;
(3)记为点C:从装有3个红球、7个白球的口袋中任取一个球,恰好是白球(这些球除颜色外完全相同);
(4)记为点D:如图2所示的正方形纸片上做随机扎针实验,则针头恰好扎在阴影区域内.
-
科目: 来源: 题型:
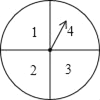
查看答案和解析>>【题目】小王和小张利用如图所示的转盘做游戏,转盘的盘面被分为面积相等的4个扇形区域,且分别标有数字1,2,3,4.游戏规则如下:两人各转动转盘一次,分别记录指针停止时所对应的数字,如两次的数字都是奇数,则小王胜;如两次的数字都是偶数,则小张胜;如两次的数字是奇偶,则为平局.解答下列问题:
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型
A
B
AB
O
人数
10
5
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?
(4)现有3个自愿献血者,2人血型为O型,1人血型为A型,若在3人中随机挑1人献血,2年后又从此3人中随机挑1人献血,试求两次所抽血型均为O型的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
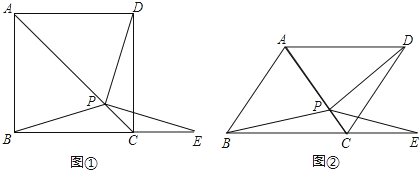
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解材料一:一组对边平行,另一组对边不平行的四边形叫梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线.梯形的中位线具有以下性质:梯形的中位线平行于两底和,并且等于两底和的一半.
如图(1):在梯形ABCD中:AD∥BC,
∵E、F是AB、CD的中点,∴EF∥AD∥BC,EF=
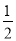 (AD+BC)
(AD+BC)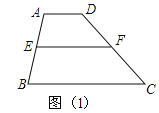
材料二:经过三角形一边的中点与另一边平行的直线必平分第三边
如图(2):在△ABC中:∵E是AB的中点,EF∥BC
∴F是AC的中点
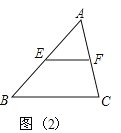
请你运用所学知识,结合上述材料,解答下列问题.
如图(3)在梯形ABCD中,AD∥BC,AC⊥BD于O,E、F分别为AB、CD的中点,∠DBC=30°.
(1)求证:EF=AC;
(2)若OD=
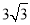 ,OC=5,求MN的长.
,OC=5,求MN的长.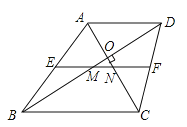
相关试题

