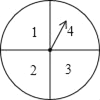
【题目】小王和小张利用如图所示的转盘做游戏,转盘的盘面被分为面积相等的4个扇形区域,且分别标有数字1,2,3,4.游戏规则如下:两人各转动转盘一次,分别记录指针停止时所对应的数字,如两次的数字都是奇数,则小王胜;如两次的数字都是偶数,则小张胜;如两次的数字是奇偶,则为平局.解答下列问题:
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
参考答案:
【答案】(1)![]() ;(2)该游戏公平.
;(2)该游戏公平.
【解析】
(1)根据概率公式直接计算即可;
(2)画树状图得出所有等可能的情况数,找出两指针所指数字都是偶数或都是奇数的概率即可得知该游戏是否公平.
解:(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率= ![]() ;
;
(2)该游戏公平.理由如下:
画树状图为:

共有16种等可能的结果数,其中两次的数字都是奇数的结果数为4,所以小王胜的概率= ![]() ;
;
两次的数字都是偶数的结果数为4,所以小张胜的概率= ![]() ,
,
因为小王胜的概率与小张胜的概率相等,
所以该游戏公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】情境观察:
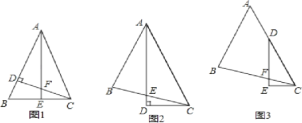
如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=
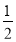 ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

A.4,30° B.2,60° C.1,30° D.3,60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN.则在点M运动过程中,线段HN长度的最小值是( )
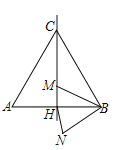
A.6B.3C.2D.1.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=60°,过点C作CD∥AB,若∠ACD=60°,求证:△ABC是等边三角形.

-
科目: 来源: 题型:
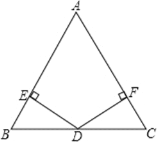
查看答案和解析>>【题目】如图,在
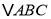 中,
中,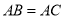 ,点
,点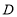 是
是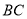 边上的中点,
边上的中点,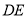 、
、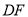 分别垂直
分别垂直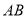 、
、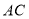 于点
于点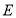 和
和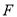 .求证:
.求证: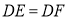
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料阅读:
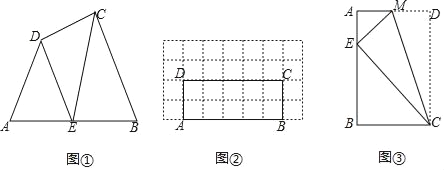
如图①,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点(无需写解答过程);
(3)如图③所示的矩形ABCD,将矩形ABCD沿CM折叠后,点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究点E的位置.
相关试题

