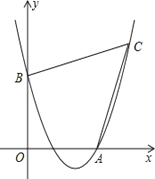
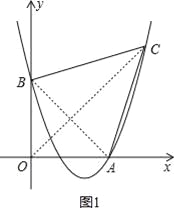
【题目】如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
参考答案:
【答案】(1)、y=![]() x2﹣
x2﹣![]() x+4;(2)、证明过程见解析;(3)、最大值为12,此时D点坐标为(2,0)
x+4;(2)、证明过程见解析;(3)、最大值为12,此时D点坐标为(2,0)
【解析】试题分析:(1)、根据抛物线经过点A(4,0),B(0,4),C(6,6),利用待定系数法,求出抛物线的表达式即可;(2)、利用两点间的距离公式分别计算出OA=4,OB=4,CB=2![]() ,CA=2
,CA=2![]() ,则OA=OB,CA=CB,根据线段垂直平分线定理的逆定理得到OC垂直平分AB,所以四边形AOBC的两条对角线互相垂直;(3)、如图2,利用两点间的距离公式分别计算出AB=4
,则OA=OB,CA=CB,根据线段垂直平分线定理的逆定理得到OC垂直平分AB,所以四边形AOBC的两条对角线互相垂直;(3)、如图2,利用两点间的距离公式分别计算出AB=4![]() ,OC=6
,OC=6![]() ,设D(t,0),根据平行四边形的性质四边形DEFG为平行四边形得到EF∥DG,EF=DG,再由OC垂直平分AB得到△OBC与△OAC关于OC对称,则可判断EF和DG为对应线段,所以四边形DEFG为矩形,DG∥OC,则DE∥AB,于是可判断△ODE∽△OAB,利用相似比得DE=
,设D(t,0),根据平行四边形的性质四边形DEFG为平行四边形得到EF∥DG,EF=DG,再由OC垂直平分AB得到△OBC与△OAC关于OC对称,则可判断EF和DG为对应线段,所以四边形DEFG为矩形,DG∥OC,则DE∥AB,于是可判断△ODE∽△OAB,利用相似比得DE=![]() t,接着证明△ADG∽△AOC,利用相似比得DG=
t,接着证明△ADG∽△AOC,利用相似比得DG=![]() (4﹣t),所以矩形DEFG的面积=DEDG=
(4﹣t),所以矩形DEFG的面积=DEDG=![]() t
t![]() (4﹣t)=﹣3t2+12t,然后根据二次函数的性质求平行四边形DEFG的面积的最大值,从而得到此时D点坐标.
(4﹣t)=﹣3t2+12t,然后根据二次函数的性质求平行四边形DEFG的面积的最大值,从而得到此时D点坐标.
试题解析:(1)、设该抛物线的解析式为y=ax2+bx+c, 根据题意得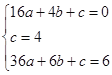 ,解得
,解得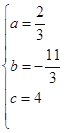 ,
,
∴抛物线的表达式为y=![]() x2﹣
x2﹣![]() x+4;
x+4;
(2)、如图1,连结AB、OC, ∵A(4,0),B(0,4),C(6,6),
∴OA=4,OB=4,CB=2![]() ,CA=2
,CA=2![]() ,
,
∴OA=OB,CA=CB, ∴OC垂直平分AB, 即四边形AOBC的两条对角线互相垂直;
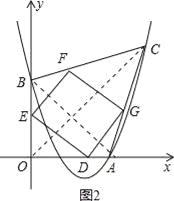
(3)、能. 如图2,AB=4![]() ,OC=6
,OC=6![]() ,设D(t,0),
,设D(t,0),
∵四边形DEFG为平行四边形, ∴EF∥DG,EF=DG, ∵OC垂直平分AB,
∴△OBC与△OAC关于OC对称, ∴EF和DG为对应线段, ∴四边形DEFG为矩形,DG∥OC,
∴DE∥AB,∴△ODE∽△OAB,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得DE=
,解得DE=![]() t, ∵DG∥OC,
t, ∵DG∥OC,
∴△ADG∽△AOC,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得DG=
,解得DG=![]() (4﹣t),
(4﹣t),
∴矩形DEFG的面积=DEDG=![]() t
t![]() (4﹣t)=﹣3t2+12t=﹣3(t﹣2)2+12,
(4﹣t)=﹣3t2+12t=﹣3(t﹣2)2+12,
当t=2时,平行四边形DEFG的面积最大,最大值为12,此时D点坐标为(2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是 ( ).
A.0既不是正数,也不是负数
B.1是绝对值最小的数
C.一个有理数不是整数就是分数
D.0的绝对值是0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面上有四个点A,B,C,D,根据下列语句画图
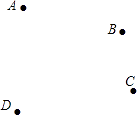
(1)画直线AB、CD交于E点;
(2)画线段AC、BD交于点F;
(3)连接AD,并将其反向延长;
(4)作射线BC. -
科目: 来源: 题型:
查看答案和解析>>【题目】林城市对教师试卷讲评课中学生参与的深度与广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
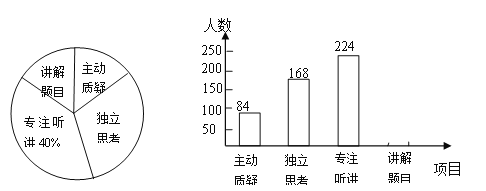
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形图补充完整;
(3)如果全市有16万名初中学生,那么在试卷评讲课中,“独立思考”的学生约有多少万人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】人无论在太阳光照射下,还是在路灯光照射下都会形成影子,那么影子的长短随时间的变化而变化的是 , 影子的长短随人的位置的变化而变化的是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式3x2-2(5+y-3x2+mx2)的值与x的值无关,则m的等于______.
相关试题

