【题目】如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α. 
(1)用含α的式子表示h(不必指出α的取值范围);
(2)当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
参考答案:
【答案】
(1)解:过点E作EH⊥AB于H,由题意四边形ACEH是矩形,
∴EH=AC=30,AH=CE=h,∠BEH=α,
∴BH=30﹣h,
在Rt△BEH中,tan∠BEH= ![]() ,
,
∴30﹣h=30tanα,
∴h=30﹣30tanα.
(2)解:当α=30°时,h=30﹣30× ![]() ≈12.7,
≈12.7,
∵12.7÷3=4.2,
∴B点的影子落在乙楼的第五层,
当B点的影子落在乙楼C处时,甲楼的影子刚好不影响乙楼采光,
此时AB=AC=30,△ABC是等腰直角三角形,
∴∠ACB=45°,
∴ ![]() =1(小时),
=1(小时),
∴从此时起1小时后甲楼的影子刚好不影响乙楼采光.
【解析】(1)过点E作EH⊥AB于H,由题意四边形ACEH是矩形,在Rt△BEH中,根据tan∠BEH= ![]() 列出方程即可解决问题.(2)①求出h的值即可解决问题,②求出∠ACB的大小即可解决问题.
列出方程即可解决问题.(2)①求出h的值即可解决问题,②求出∠ACB的大小即可解决问题.
【考点精析】利用平行投影对题目进行判断即可得到答案,需要熟知太阳光线可以看成是平行光线,平行光线所形成的投影称为平行投影;作物体的平行投影:由于平行投影的光线是平行的,而物体的顶端与影子的顶端确定的直线就是光线,故根据另一物体的顶端可作出其影子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D
(1)如图1,求证:BD=ED;
(2)如图2,AD为⊙O的直径.若BC=6,sin∠BAC= ,求OE的长.
,求OE的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=
 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N. 
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=
 AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE. 
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:
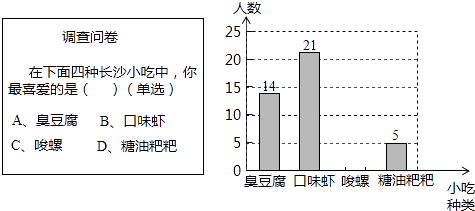
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1

(1)在网格中画出△A1B1C1;
(2)计算线段AC在变换到A1C1的过程中扫过区域的面积(重叠部分不重复计算). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2
 ,则图中阴影部分面积是(结果保留π和根号)
,则图中阴影部分面积是(结果保留π和根号) 
相关试题

