【题目】已知⊙O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D
(1)如图1,求证:BD=ED; 
(2)如图2,AD为⊙O的直径.若BC=6,sin∠BAC= ![]() ,求OE的长.
,求OE的长. 
参考答案:
【答案】
(1)证明:连接BE.
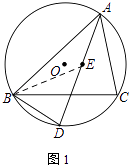
∵是△ABC的内心,
∴∠ABE=∠CBE,∠BAD=∠CAD.
∵∠DBC=∠CAD.
∴∠DBC=∠BAD.
∵∠BED=∠BAD+∠ABE,
∴∠DBE=∠DEB.
∴BD=ED.
(2)解:如图2所示;连接OB.
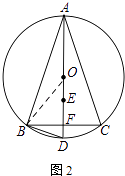
∵AD是直径,A平分∠BAC,
∴AD⊥BC,且BD=FC=3.
∵∠BAC=∠BOD,sin∠BAC= ![]() ,BF=3,
,BF=3,
∴OB=5.
∵在Rt△BOF中,BF=3,OB=5,
∴OF= ![]() =4.
=4.
∴DF=1.
在Rt△BDF中,BF2+DF2=BD2.
∴BD= ![]() .
.
∴DE= ![]() .
.
使用OE=5﹣ ![]() .
.
【解析】(1)连接BE.依据三角形的内心的性质以及圆周角定理证明∠DBE=∠DEB即可;(2)连接OB.先证明圆周角定理和三角形的内心的性质可知∠BAC=∠BOF,依据锐角三角函数的定义可求得OB的长,然后依据勾股定理可求得OF的长于是得到DF的长,接下来,在△BDF中,由勾股定理可求得BD的长,依据问题(1)的结论可得到DE的长,从而求得OE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是( )

A.△PAB∽△PCA
B.△PAB∽△PDA
C.△ABC∽△DBA
D.△ABC∽△DCA -
科目: 来源: 题型:
查看答案和解析>>【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
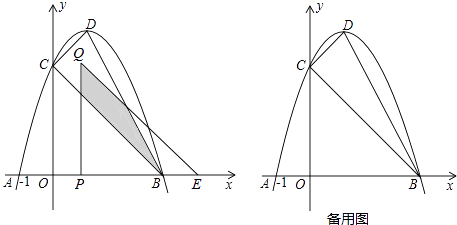
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=
 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N. 
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=
 AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE. 
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α.

(1)用含α的式子表示h(不必指出α的取值范围);
(2)当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
相关试题

