【题目】月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值.
(3)假设公司的这种电子产品第一年恰好按年利润s(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格x(元)定在8元以上(x>8),当第二年的年利润不低于103万元时,请结合年利润s(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.

参考答案:
【答案】(1)y= ;(2)当每件的销售价格定为16元时,第一年年利润的最大值为﹣16万元;(3)图见解析,当11≤x≤21时,第二年的年利润s不低于103万元.
;(2)当每件的销售价格定为16元时,第一年年利润的最大值为﹣16万元;(3)图见解析,当11≤x≤21时,第二年的年利润s不低于103万元.
【解析】试题分析:(1)依据待定系数法,即可求出y(万件)与x(元/件)之间的函数关系式;
(2)分两种情况进行讨论,当x=8时,zmax=-80;当x=16时,zmax=-16;根据-16>-80,可得当每件的销售价格定为16元时,第一年年利润的最大值为-16万元.
(3)根据第二年的年利润z=(x-4)(-x+28)-16=-x2+32x-128,令z=103,可得方程103=-x2+32x-128,解得x1=11,x2=21,然后在平面直角坐标系中,画出z与x的函数图象,根据图象即可得出销售价格x(元/件)的取值范围.
试题解析:(1)当4≤x≤8时,设y=![]() ,将A(4,40)代入得k=4×40=160,
,将A(4,40)代入得k=4×40=160,
∴y与x之间的函数关系式为y=![]() ;
;
当8<x≤28时,设y=k'x+b,将B(8,20),C(28,0)代入,
得: ![]() ,解得
,解得![]() ,
,
∴y与x之间的函数关系式为y=﹣x+28,
综上所述,y=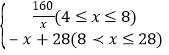 ;
;
(2)当4≤x≤8时,s=(x﹣4)y﹣160=(x﹣4)![]() ﹣160=﹣
﹣160=﹣![]() ,
,
∵当4≤x≤8时,s随着x的增大而增大,
∴当x=8时,smax=﹣![]() =﹣80;
=﹣80;
当8<x≤28时,s=(x﹣4)y﹣160=(x﹣4)(﹣x+28)﹣160=﹣(x﹣16)2﹣16,
∴当x=16时,smax=﹣16;
∵﹣16>﹣80,
∴当每件的销售价格定为16元时,第一年年利润的最大值为﹣16万元.
(3)∵第一年的年利润为﹣16万元,
∴16万元应作为第二年的成本,
又∵x>8,
∴第二年的年利润s=(x﹣4)(﹣x+28)﹣16=﹣x2+32x﹣128,
令s=103,则103=﹣x2+32x﹣128,
解得x1=11,x2=21,
在平面直角坐标系中,画出s与x的函数示意图可得:
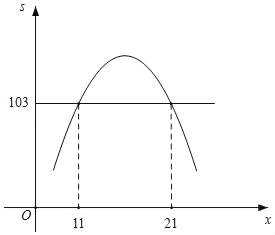
观察示意图可知,当s≥103时,11≤x≤21,
∴当11≤x≤21时,第二年的年利润s不低于103万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.
(1)求证:△AOC≌△CEB;
(2)求△ABD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为任意三角形,以AB、AC为边分别向外做等边△ABD和等边△ACE,连接CD、BE并相交于点P.求证:
(1)CD=BE;
(2)∠BPC=120°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.

(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)它们出发
 小时时,离各自出发地的距离相等,求乙车离出发地的距离y乙(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
小时时,离各自出发地的距离相等,求乙车离出发地的距离y乙(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

-
科目: 来源: 题型:
查看答案和解析>>【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.则结论:①BE=EC;②∠EDC=∠ECD;③∠B=∠BDE;④△ABC∽△ACD;⑤△DEC是等边三角形.其中正确的结论有( )
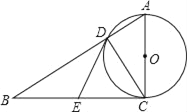
A. 2个 B. 3个 C. 4个 D. 5个
相关试题

