【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长度为50m .设饲养室为长为x(m),占地面积为![]() .
.
(1)如图![]() ,问饲养室为长x为多少时,占地面积y 最大?
,问饲养室为长x为多少时,占地面积y 最大?
(2)如图![]() ,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.
,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.


参考答案:
【答案】(1)x=25;(2)小敏的说法不正确.
【解析】
试题分析:(1)根据题意用含x的代数式表示出饲养室的宽,由矩形的面积=长×宽计算即可;
(2)由(1)可知y是x的二次函数,根据二次函数的性质分析即可.
试题解析:(1)∵![]() =
=![]() ,∴当x=25时,占地面积y最大;
,∴当x=25时,占地面积y最大;
(2)![]() =
=![]() ,∴当x=26时,占地面积y最大.即当饲养室长为26m时,占地面积最大.∵26-25=1≠2,∴小敏的说法不正确.
,∴当x=26时,占地面积y最大.即当饲养室长为26m时,占地面积最大.∵26-25=1≠2,∴小敏的说法不正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据5,7,8,8,9的众数是( )
A.5
B.7
C.8
D.9、 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图像如图,顶点坐标D为(3,
的图像如图,顶点坐标D为(3,  )。它与
)。它与 轴交于A,B两点(点A在B的左侧),与
轴交于A,B两点(点A在B的左侧),与 轴交于C点,且AB的长为12. 动点P从A点出发,沿AB方向以1个单位长度/秒的速度向点B运动,设运动时间为t秒.
轴交于C点,且AB的长为12. 动点P从A点出发,沿AB方向以1个单位长度/秒的速度向点B运动,设运动时间为t秒.(1)求二次函数的解析式;
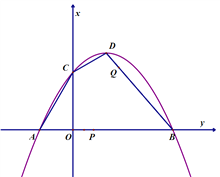
(2)当△PDB为等腰三角形时,求t的值;
(3)若动点Q与P同时从A点出发,点Q沿折线ACCDDB运动,在AC,CD,DB上运动的速度分别为3,
 ,2 (个单位长度/秒)﹒当P,Q中的一点到达B点时,两点同时停止运动.连结PQ.
,2 (个单位长度/秒)﹒当P,Q中的一点到达B点时,两点同时停止运动.连结PQ.①当PQ的中点恰好落在y轴上时,求t的值;
②在P,Q的运动过程中,若线段PQ的垂直平分线与线段BD有交点时,请直接写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列的点在第二象限的是( )
A. (2,3)B. (﹣2,3)C. (2,﹣3)D. (﹣2,﹣3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m2+m-1=0,则m3+2m2+2018的值为( )
A. 2020 B. 2017 C. 2019 D. 2015
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二元一次方程2x﹣y=3,用含x的式子表示y的形式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D落在AB边上,斜边DE交AC于点F,则n的大小和图中阴影部分的面积分别为( )

A. 30,2 B. 60,2 C. 60,
 D. 60,
D. 60, 
相关试题

