搜索
【题目】将一副三角板放在同一平面内，使直角顶点重合于点O
（1）如图①，若∠AOB=155°，求∠AOD、∠BOC、∠DOC的度数.
（2）如图①，你发现∠AOD与∠BOC的大小有何关系？∠AOB与∠DOC有何关系？直接写出你发现的结论.
（3）如图②，当△AOC与△BOD没有重合部分时，（2）中你发现的结论是否还仍然成立，请说明理由.
参考答案：
【答案】(1)
(2) ∠AOD与∠BOC的大小关系为：
∠AOB与∠DOC存在的数量关系为：
(3)仍然成立.
【解析】
（1）先计算出
再根据
（2）根据(1)中得出的度数直接写出结论即可.
（3）根据
即可得到
利用周角定义得∠AOB+∠COD+∠AOC+∠BOD=360°，而∠AOC=∠BOD=90°，即可得到∠AOB+∠DOC=180°．
(1)∵
而
同理：
∴
∴
(2) ∠AOD与∠BOC的大小关系为： ∠AOB与∠DOC存在的数量关系为：
(3) 
仍然成立.
理由如下：∵
又∵
∴
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC三条边的长度分别是
，
，
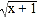，记△ABC的周长为C△ABC．（1）当x＝2时，△ABC的最长边的长度是 （请直接写出答案）；
（2）请求出C△ABC（用含x的代数式表示，结果要求化简）；
（3）我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式：S＝
．其中三角形边长分别为a，b，c，三角形的面积为S．若x为整数，当C△ABC取得最大值时，请用秦九韶公式求出△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店销售一种销售成本为40元/千克的水产品，若 50元 /千克销售，一个月可售出500千克，销售价每涨价1元，月销售量就减少10千克．
（1）写出月销售利润y（单位：元） 与售价x（单位：元/千克） 之间的函数解析式．
（2）当售价定为多少时会获得最大利润？求出最大利润．
（3）商店想在月销售成本不超过10000元的情况下，使月销售利润达到8000元销售单价应定为多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，O为直线AB上一点，∠COE=90°,OF平分∠AOE.
（1）若∠COF=40°，求∠BOE的度数.
（2）若∠COF=α（0°＜α＜90°），则∠BOE=______（用含α的式子表示）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，E是等边三角形ABC的边AB所在直线上一点，D是边BC所在直线上一点，且D与C不重合，若EC＝ED．则称D为点C关于等边三角形ABC的反称点，点E称为反称中心．
在平面直角坐标系xOy中，
（1）已知等边三角形AOC的顶点C的坐标为（2，0），点A在第一象限内，反称中心E在直线AO上，反称点D在直线OC上．
①如图2，若E为边AO的中点，在图中作出点C关于等边三角形AOC的反称点D，并直接写出点D的坐标： ；
②若AE＝2，求点C关于等边三角形AOC的反称点D的坐标；
（2）若等边三角形ABC的顶点为B（n，0），C（n+1，0），反称中心E在直线AB上，反称点D在直线BC上，且2≤AE＜3．请直接写出点C关于等边三角形ABC的反称点D的横坐标t的取值范围： （用含n的代数式表示）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】四川雅安发生地震后，某校学生会向全校1900名学生发起了“心系雅安”捐款活动，为了解捐款情况，学会生随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列是问题：
（1）本次接受随机抽样调查的学生人数为 ，图①中m的值是 ；
（2）求本次调查获取的样本数据的平均数、众数和中位数；
（3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，长方形纸片ABCD的长AD＝9cm，宽AB＝3cm，将其折叠，使点D与点B重合．
求：（1）折叠后DE的长；（2）以折痕EF为边的正方形面积．
相关试题
