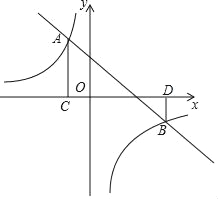
【题目】如图,直线y=﹣x+2与反比例函数y=![]() (k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(1)求a,b的值及反比例函数的解析式;
(2)若点P在直线y=﹣x+2上,且S△ACP=S△BDP,请求出此时点P的坐标;
(3)在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.
参考答案:
【答案】(1)y=![]() ;(2)P(0,2)或(-3,5);(3)M(
;(2)P(0,2)或(-3,5);(3)M(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)利用点在直线上,将点的坐标代入直线解析式中求解即可求出a,b,最后用待定系数法求出反比例函数解析式;
(2)设出点P坐标,用三角形的面积公式求出S△ACP=![]() ×3×|n+1|,S△BDP=
×3×|n+1|,S△BDP=![]() ×1×|3n|,进而建立方程求解即可得出结论;
×1×|3n|,进而建立方程求解即可得出结论;
(3)设出点M坐标,表示出MA2=(m+1)2+9,MB2=(m3)2+1,AB2=32,再三种情况建立方程求解即可得出结论.
(1)∵直线y=-x+2与反比例函数y=![]() (k≠0)的图象交于A(a,3),B(3,b)两点,∴-a+2=3,-3+2=b,
(k≠0)的图象交于A(a,3),B(3,b)两点,∴-a+2=3,-3+2=b,
∴a=-1,b=-1,
∴A(-1,3),B(3,-1),
∵点A(-1,3)在反比例函数y=![]() 上,
上,
∴k=-1×3=-3,
∴反比例函数解析式为y=![]() ;
;
(2)设点P(n,-n+2),
∵A(-1,3),
∴C(-1,0),
∵B(3,-1),
∴D(3,0),
∴S△ACP=![]() AC×|xPxA|=
AC×|xPxA|=![]() ×3×|n+1|,S△BDP=
×3×|n+1|,S△BDP=![]() BD×|xBxP|=
BD×|xBxP|=![]() ×1×|3n|,
×1×|3n|,
∵S△ACP=S△BDP,
∴![]() ×3×|n+1|=
×3×|n+1|=![]() ×1×|3n|,
×1×|3n|,
∴n=0或n=3,
∴P(0,2)或(3,5);
(3)设M(m,0)(m>0),
∵A(1,3),B(3,1),
∴MA2=(m+1)2+9,MB2=(m3)2+1,AB2=(3+1)2+(13)2=32,
∵△MAB是等腰三角形,
∴①当MA=MB时,
∴(m+1)2+9=(m3)2+1,
∴m=0,(舍)
②当MA=AB时,
∴(m+1)2+9=32,
∴m=1+![]() 或m=1
或m=1![]() (舍),
(舍),
∴M(1+![]() ,0)
,0)
③当MB=AB时,(m3)2+1=32,
∴M(3+![]() ,0)
,0)
即:满足条件的M(1+![]() ,0)或(3+
,0)或(3+![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于受到手机更新换代的影响,某店经销的甲型号手机今年的售价比去年每台降价500元.如果卖出相同数量的手机,那么去年销售额为8万元,今年销售额只有6万元.
(1)今年甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划购进乙型号手机销售,已知甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台,请问有几种进货方案?
-
科目: 来源: 题型:
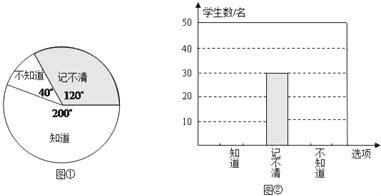
查看答案和解析>>【题目】今年苏州市在全市中小学中开展以感恩和生命为主题的教育活动,各中小学结合学生实际,开展了形式多样的感恩教育活动.下面图①,图②分别是某校调查部分学生是否知道母亲生日情况的扇形统计图和条形统计图.根据图上信息,解答下列问题:
(1)求本次被调查学生的人数,并补全条形统计图;
(2)若全校共有2700名学生,你估计这所学校有多少名学生知道母亲的生日?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是
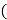

A. 55° B. 60° C. 65° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价
 元。据此规律,请回答:
元。据此规律,请回答:(1)商场日销售量增加_____件,每件商品盈利_____元(用含
 的代数式表示)。
的代数式表示)。(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球运动是同学们非常喜欢的日常体育运动,为了更合理地配置体育运动器材和场地,某校针对“你最喜欢的球类运动”进行了一次随机抽样调查(每名被调查者分别选一项球类运动),并把调查结果绘制成如图的两个统计图表(不完整).
某校学生最喜爱的球类运动统计表
最喜爱的球类运动
人数
足球
27
篮球
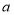
乒乓球
24
羽毛球
24
排球
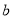
某校学生最喜爱的球类运动统计图

请根据所给信息,解答下列问题:
(1)本次被抽样调查的学生共有多少人?
(2)求扇形统计图中最喜爱篮球部分的圆心角度数;
(3)若该校共有学生960人,请根据抽样结果估计学生中最喜爱乒乓球的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.

(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.
相关试题

