【题目】【探究】如图①,分别以△ABC的两边AB和AC为边向△ABC外作正三角形ABD和正三角形ACE,连结DC、BE.求证:DC=BE.
【拓展】如图②,在四边形ABCD中,AB=BC=5,∠ABC=45°,连结AC、BD.若∠DAC=90°,AC=AD,则BD的长为_____.

参考答案:
【答案】证明见解析;拓展: ![]()
【解析】试题分析:由等边三角形性质,根据三角形全等的判定SAS,可证明;
(2)过A作等腰直角三角形EAB,∠EAB=∠EBC=90°,连接EC,可证明△EAC≌△DAB,根据勾股定理求得BE=![]() ,然后再次由勾股定理解答即可.
,然后再次由勾股定理解答即可.

试题解析:【探究】∵△ABD和△ACE是等边三角形,
∴AD = AB,AC=AE,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE.
∴△ADC≌△ABE.
∴DC= BE.
【拓展】![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级共有150名男生,从中随机抽取30名男生在“阳光体育活动”启动日进行“引体向上”测试,下表是测试成绩记录(单位:个):
3
2
1
2
3
3
5
2
2
4
2
4
2
5
2
3
4
4
1
3
3
2
5
1
4
2
3
1
2
4
(1)我们已经会列频数分布表、画条形统计图、折线统计图和扇形统计图.为了能让体育老师一目了然知道整个测试情况,请你选择一种合适的统计表或统计图整理表示上述数据;
(2)观察分析(1)中的统计表或统计图,请你写出两条从中获得的信息:
(3)规定八年级男生“引体向上”4个及以上为合格.若学校准备对“引体向上”不合格的男生提出锻炼建议,试估计要对八年级多少名男生提出这项建议? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,平行于x轴的直线与抛物线y=ax(a>0)相交于A、B两点.设点B的横坐标为m(m>0).
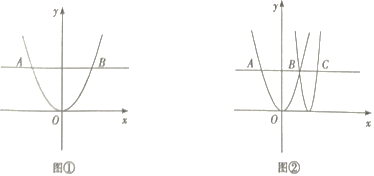
(1)求AB的长(用含m的代数式表示).
(2)如图②,点C在直线AB上,点C的横坐标为2m.若a=1,m=2,求顶点在x轴上且经过B、C两点的抛物线的顶点坐标.
(3)点D在直线AB上,BD=2AB,过O、B、D三点的抛物线的顶点为P,其对应函数的二次项系数为a1.
①求
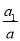 的值.
的值.②当m=2,△BPD为等腰直角三角形,直接写出a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校“沥园文学”社成员来自初一、初二、初三三个年级的学生,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自初一的学生为10人,则下列说法不正确的是( )
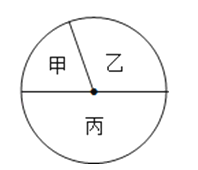
A.扇形甲的圆心角是72°
B.学生的总人数是90人
C.初三的人数比初二的人数多10人
D.初一的人数比初三的人数少15人 -
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2﹣4x=5时,此方程可变形为( )
A.(x+2)2=1
B.(x﹣2)2=1
C.(x+2)2=9
D.(x﹣2)2=9 -
科目: 来源: 题型:
查看答案和解析>>【题目】为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
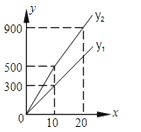
(1)观察图象求a,b,m的值
(2)直接写出y1 , y2与x之间的函数关系式;
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A,B两个团队合计50人,求A,B两个团队各有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】下表记录了某种幼树在一定条件下移植成活情况
移植总数n
400
1500
3500
7000
9000
14000
成活数m
325
1336
3203
6335
8073
12628
成活的频率(精确到0.01)
0.813
0.891
0.915
0.905
0.897
0.902
由此估计这种幼树在此条件下移植成活的概率约是_____(精确到0.1).
相关试题

