【题目】如图,点B为AC上一点,分别以AB,BC为边在AC同侧作等边三角形ABD和等边三角形BCE,点P,M,N分别为AC,AD,CE的中点.
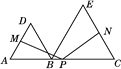
(1)求证:PM=PN;
(2)求∠MPN的度数.
参考答案:
【答案】(1)证明见解析;(2) ∠MPN=120°.
【解析】试题分析:(1)连接CD、AE,由△ABD和△BCE是等边三角形得AB=DB,BE=BC,∠ABD=∠CBE=60°,易证△ABE≌△DBC,得AE=DC,再由三角形中位线的性质可证PM=PN;
(2)如图,设PM交AE于F,PN交CD于G,AE交CD于H,易证四边形PFHG为平行四边形,故∠MPN=120°.
试题解析:(1)如图,连接CD,AE.由三角形中位线定理可得PM=![]() CD,PN=
CD,PN=![]() AE,∵△ABD和△BCE是等边三角形,∴AB=DB,BE=BC,∠ABD=∠CBE=60°,∴∠ABE=∠DBC.
AE,∵△ABD和△BCE是等边三角形,∴AB=DB,BE=BC,∠ABD=∠CBE=60°,∴∠ABE=∠DBC.
∴△ABE≌△DBC,∴AE=DC.∴PM=PN.
(2)如图,设PM交AE于F,PN交CD于G,AE交CD于H.由(1)知△ABE≌△DBC,∴∠BAE=∠BDC.
∴∠AHD=∠ABD=60°,∴∠FHG=120°.
易证四边形PFHG为平行四边形,∴∠MPN=120°.
-
科目: 来源: 题型:
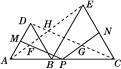
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点且BE平分∠ABD,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
求证:
(1)∠BAD=2∠DAC
(2)EF=EG.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮在计算一个多项式与3x2﹣2x+7的差时,因误以为是加上3x2﹣2x+7而得到答案5x2+2x+4,请求出这个问题的正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两个内角之和小于第三个内角,那么该三角形是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 都有可能
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图1,平行四边形ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.

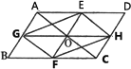
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF//AB,GH//BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,BA=BC,△BEF为等腰直角三角形,∠BEF=90°,M为AF的中点,求证:ME=
 CF.
CF.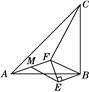
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年春节联欢晚会分为A(语言类)、B(歌舞类)、C(魔术类)、D(杂技类)四类节目.为了了解某养老院老人对这几类节目的喜好程度,民政部门在该养老院随机抽取部分老人进行了问卷调查,规定每位老人只能选一类自己最喜欢的节目,并制成了以下两幅不完整的统计图.由图中所给出的信息解答下列问题:
(1)补全条形统计图;
(2)已知该养老院共有230位老人,请你估计该养老院喜欢语言类节目的老人大约有多少人?

相关试题

