【题目】已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.
(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:如图所示,
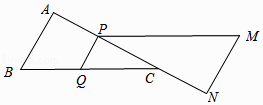
AB=3cm,BC=5cm,AC⊥AB,
∴Rt△ABC中,AC=4,
若PQ∥AB,则有 ![]() =
= ![]() ,
,
∵CQ=PA=t,CP=4﹣t,QB=5﹣t,
∴ ![]() =
= ![]() ,
,
即20﹣9t+t2=t2,
解得t= ![]() ,
,
当t= ![]() 时,PQ∥AB
时,PQ∥AB
(2)
解:如图所示,过点P作PD⊥BC于点D,
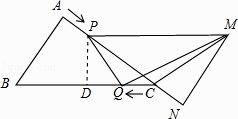
∴∠PDC=∠A=90°,
∵∠PCD=∠BCA
∴△CPD∽△CBA,
∴ ![]() =
= ![]() ,
,
当t=3时,CP=4﹣3=1,
∵BA=3,BC=5,
∴ ![]() =
= ![]() ,
,
∴PD= ![]() ,
,
又∵CQ=3,PM∥BC,
∴S△QMC= ![]() ×3×
×3× ![]() =
= ![]() ;
;
(3)
解:存在时刻t= ![]() ,使PQ⊥MQ,
,使PQ⊥MQ,
理由如下:如图所示,过点M作ME⊥BC的延长线于点E,
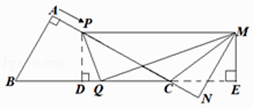
∵△CPD∽△CBA,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵BA=3,CP=4﹣t,BC=5,CA=4,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴PD= ![]() (4﹣t),CD=
(4﹣t),CD= ![]() (4﹣t).
(4﹣t).
∵PQ⊥MQ,
∴∠PDQ=∠QEM=90°,∠PQD=∠QME,
∴△PDQ∽△QEM,
∴ ![]() =
= ![]() ,即PDEM=QEDQ.
,即PDEM=QEDQ.
∵EM=PD= ![]() (4﹣t)=
(4﹣t)= ![]() ﹣
﹣ ![]() t,
t,
DQ=CD﹣CQ= ![]() (4﹣t)﹣t=
(4﹣t)﹣t= ![]() ﹣
﹣ ![]() t,
t,
QE=DE﹣DQ=5﹣[ ![]() (4﹣t)﹣t]=
(4﹣t)﹣t]= ![]() +
+ ![]() t,
t,
∴( ![]() ﹣
﹣ ![]() t)2=(
t)2=( ![]() ﹣
﹣ ![]() t)(
t)( ![]() +
+ ![]() t),
t),
即2t2﹣3t=0,
∴t= ![]() 或t=0(舍去),
或t=0(舍去),
∴当t= ![]() 时,PQ⊥MQ.
时,PQ⊥MQ.
【解析】(1)根据勾股定理求出AC,根据PQ∥AB,得出关于t的比例式,求解即可;(2)过点P作PD⊥BC于D,根据△CPD∽△CBA,列出关于t的比例式,表示出PD的长,再根据S△QMC= ![]() QCPD,进行计算即可;(3)过点M作ME⊥BC的延长线于点E,根据△CPD∽△CBA,得出PD=
QCPD,进行计算即可;(3)过点M作ME⊥BC的延长线于点E,根据△CPD∽△CBA,得出PD= ![]() (4﹣t),CD=
(4﹣t),CD= ![]() (4﹣t),再根据△PDQ∽△QEM,得到
(4﹣t),再根据△PDQ∽△QEM,得到 ![]() =
= ![]() ,即PDEM=QEDQ,进而得到方程(
,即PDEM=QEDQ,进而得到方程( ![]() ﹣
﹣ ![]() t)2=(
t)2=( ![]() ﹣
﹣ ![]() t)(
t)( ![]() +
+ ![]() t),求得t=
t),求得t= ![]() 或t=0(舍去),即可得出当t=
或t=0(舍去),即可得出当t= ![]() 时,PQ⊥MQ.
时,PQ⊥MQ.
【考点精析】关于本题考查的相似三角形的应用,需要了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工艺品厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况 (超产记为正,减产记为负):

(1) 写出该厂星期一生产工艺品的数量.
(2) 本周产量最多的一天比最少的一天多生产多少个工艺品?
(3) 请求出该工艺品厂在本周实际生产工艺品的数量.
(4) 已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个可得50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为支持四川抗震救灾,重庆市A、B、C三地现在分别有赈灾物资100吨、100吨、80吨,需要全部运往四川重灾地区的D、E两县.根据灾区的情况,这批赈灾物资运往D县的数量比运往E县的数量的2倍少20吨.
(1)求这批赈灾物资运往D、E两县的数量各是多少?
(2)若要求C地运往D县的赈灾物资为60吨,A地运往D的赈灾物资为x吨(x为整数),B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍.其余的赈灾物资全部运往E县,且B地运往E县的赈灾物资数量不超过25吨.则A、B两地的赈灾物资运往D、E两县的方案有几种?请你写出具体的运送方案;
(3)已知A、B、C三地的赈灾物资运往D、E两县的费用如下表:A地
B地
C地
运往D县的费用(元/吨)
220
200
200
运往E县的费用(元/吨)
250
220
210
为及时将这批赈灾物资运往D、E两县,某公司主动承担运送这批赈灾物资的总费用,在(2)问的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?
-
科目: 来源: 题型:
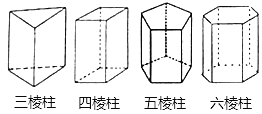
查看答案和解析>>【题目】如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有 个面, 条棱, 个顶点;
(2)六棱柱有 个面, 条棱, 个顶点;
(3)由此猜想n棱柱有 个面, 条棱, 个顶点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料后解决问题:
小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)(22+1)(24+1)(28+1)
=(2+1)(2﹣1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1)=_____.
(2)(3+1)(32+1)(34+1)(38+1)(316+1)=_____.
(3)化简:(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).
-
科目: 来源: 题型:
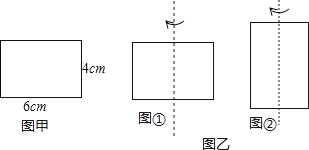
查看答案和解析>>【题目】探究:有一长6cm,宽4cm的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:
方案一:以较长的一组对边中点所在直线为轴旋转,如图①;
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)如果该矩形的长宽分别是5cm和3cm呢?请通过计算说明哪种方法构造的圆柱体积大;
(3)通过以上探究,你发现对于同一个矩形(不包括正方形),以其一组对边中点所在直线为轴旋转得到一个圆柱,怎样操作所得到的圆柱体积大(不必说明原因)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体=
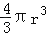 ,V圆锥=
,V圆锥=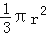 h)
h)(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是?
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着它的斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
相关试题

