【题目】如图,在Rt△ABC中,点D在直角边BC上,DE平分∠ADB,∠1=∠2=∠3,AC=5cm.
(1)求∠3的度数;
(2)判断DE与AB的位置关系,并说明理由;
(3)求BE的长.

参考答案:
【答案】(1)∠3=30°;(2)DE⊥AB;(3)BE=5cm.
【解析】
(1)根据三角形内角和定理解答;
(2)根据已知条件∠2=∠3、DE平分∠ADB,可以判定DE是等腰△ABD底边AB上的中垂线,即DE⊥AB;
(3)利用(1)中的30°的∠3所对的直角边是斜边的一半知AC=![]() AB;然后根据(2)中的DE是边AB的中垂线的性质知BE=
AB;然后根据(2)中的DE是边AB的中垂线的性质知BE=![]() AB;所以BE=AC=5cm.
AB;所以BE=AC=5cm.
解:(1)在Rt△ABC中,∠C=90°,∠1=∠2=∠3,
∴∠1+∠2+∠3=90°,即3∠3=90°,
∴∠3=30°;
(2)DE⊥AB.
理由:在△ADB中,∠2=∠3,
∴△ADB是等腰三角形;
又∵DE平分∠ADB,
∴DE是边AB上的中垂线,
∴DE⊥AB;
(3)由(1)知,Rt△ABC中,∠3=30°,
∴AC=![]() AB(30°角所对的直角边是斜边的一半);
AB(30°角所对的直角边是斜边的一半);
又由(2)知,DE是边AB上的中垂线,
∴BE=![]() AB,
AB,
∴BE=AC=5cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,并在∠MON内部作射线OC.
(1)如图1,三角板的一边ON与射线OB重合,且∠AOC=150°.若以点O为观察中心,射线OM表示正北方向,求射线OC表示的方向;
(2)如图2,将三角板放置到如图位置,使OC恰好平分∠MOB,且∠BON=2∠NOC,求∠AOM的度数;
(3)若仍将三角板按照如图2的方式放置,仅满足OC平分∠MOB,试猜想∠AOM与∠NOC之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织甲、乙两队开展“保护生态环境知识竞赛”,满分为10分,得分均为整数,规定得分达到6分及以上为合格,达到9分及以上为优秀,如图是甲、乙两队学生这次竞赛成绩分布条形统计图.
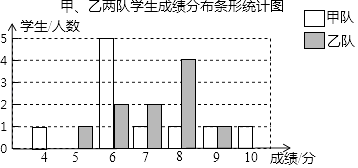
根据以上信息,请解答下面的问题:
(1)在下面甲、乙两队的成绩统计表中,a= , b=c= .平均分
中位数
众数
方差
合格率
优秀率
甲队
a
6
c
2.76
90%
20%
乙队
7.2
b
8
1.36
80%
10%
(2)小华同学说:“我在这次比赛中得到了7分,这在我所在的小队成绩中属于中等偏上的位置!”观察(1)中的表格,小华是队的学生;(填“甲”或“乙”)
(3)甲队同学认为:甲队的合格率、优秀率均高于乙队,所以甲队的成绩好于乙队.但乙队同学不同意甲队同学的说法,认为乙队的成绩要好于甲队.请你写出两条支持乙队同学观点的理由.
(4)学校要从从甲、乙两队获得优秀的学生中,选取两名同学参加市级比赛,则恰好同时选中的两人均为甲队学生的概率为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
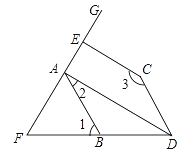
(1)请说明∠1=∠BDC;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式3x6﹣2x2﹣4的常数项为a,次数为b.
(1)设a与b分别对应数轴上的点A、点B,请直接写出a= ,b= ,并在数轴上确定点A、点B的位置;
(2)在(1)的条件下,点P以每秒2个单位长度的速度从点A向B运动,运动时间为t秒:
①若PA﹣PB=6,求t的值,并写出此时点P所表示的数;
②若点P从点A出发,到达点B后再以相同的速度返回点A,在返回过程中,求当OP=3时,t为何值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,AB=2
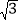 ,∠A=120°,点P、Q、K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
,∠A=120°,点P、Q、K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )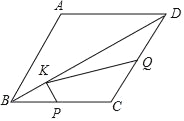
A. 1 B. 3 C.
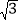 D.
D. 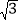 +1
+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填写下表,观察被开方数a的小数点与算术平方根
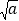 的小数点的移动规律:
的小数点的移动规律:a
0.0016
0.16
16
1600
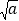
(2)根据你发现的规律填空:
①已知:
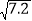 =2.683 ,
=2.683 ,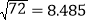 则
则 =_________,
=_________, 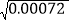 =________
=________②已知:
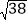 =6.164,若
=6.164,若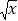 =61.64, 则x=____________,
=61.64, 则x=____________,(3)直接写出
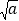 与a的大小.
与a的大小.
相关试题

