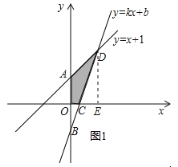
【题目】如图,已知函数 y=x+1 的图象与 y 轴交于点 A,一次函数 y=kx+b 的图象经过点 B(0,﹣1),与x 轴 以及 y=x+1 的图象分别交于点 C、D,且点 D 的坐标为(1,n),

(1)则n= ,k= ,b= ;
(2)函数 y=kx+b 的函数值大于函数 y=x+1 的函数值,则X的取值范围是 ;
(3)求四边形 AOCD 的面积;
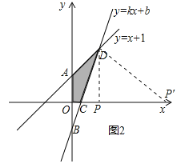
(4)在 x轴上是否存在点 P,使得以点 P,C,D 为顶点的三角形是直角三角形?若存在求出点 P 的坐标; 若不存在,请说明理由.
参考答案:
【答案】(1)2,3,-1;(2)![]() ;(3)
;(3)![]() (4)
(4)![]() 或
或![]()
【解析】
试题分析:(1)对于直线![]() ,令
,令![]() 求出
求出![]() 的值,确定出A的坐标,把B坐标代入
的值,确定出A的坐标,把B坐标代入![]() 中求出b的值,再将D坐标代入
中求出b的值,再将D坐标代入![]() 求出n的值,进而将D坐标代入求出
求出n的值,进而将D坐标代入求出![]() 的值即可;
的值即可;
由两个一次函数解析式,结合图象确定出![]() 的范围;
的范围;
过D作![]() 垂直于
垂直于![]() 轴,四边形
轴,四边形![]() 的面积等于梯形
的面积等于梯形![]() 面积减去三角形
面积减去三角形![]() 面积,求出即可;
面积,求出即可;
在![]() 轴上存在点P,使得以点P、C、D为顶点的三角形是直角三角形,理由:分两种情况考虑:
轴上存在点P,使得以点P、C、D为顶点的三角形是直角三角形,理由:分两种情况考虑:![]() ;
;![]() ,分别求出P点坐标即可.
,分别求出P点坐标即可.
试题解析:(1)对于直线![]() ,令
,令![]() 得到
得到![]() ,即A(0,1),把B(0,-1)代入
,即A(0,1),把B(0,-1)代入![]() 中,得:
中,得:![]() ,把D(1,n)代入
,把D(1,n)代入![]() 得:
得:![]() ,即D(1,2),把D坐标代入
,即D(1,2),把D坐标代入![]() 中得:
中得:![]() ,即
,即![]() ,故答案为:2,3,-1;
,故答案为:2,3,-1;
一次函数![]() 与
与![]() 交于点D(1,2),由图象得:函数
交于点D(1,2),由图象得:函数![]() 的函数值大于函数
的函数值大于函数![]() 的函数值
的函数值![]() 时的取值范围是
时的取值范围是![]() ;故答案为:
;故答案为:![]() ;
;
过D作![]() 垂直于
垂直于![]() 轴,如图1所示,则
轴,如图1所示,则![]()
![]()
![]()
(4)如图2,在![]() 轴上存在点P,使得以点P、C、D为顶点的三角形是直角三角形,理由:分两种情况考虑:当
轴上存在点P,使得以点P、C、D为顶点的三角形是直角三角形,理由:分两种情况考虑:当![]() 时,可得
时,可得![]()
![]() 斜率为3,
斜率为3,![]() 斜率为
斜率为![]() ,
,![]()
![]() 解析式为
解析式为![]() 令
令![]() 即
即![]() 当
当![]() 时,由D横坐标为1,得到P点横坐标为1,
时,由D横坐标为1,得到P点横坐标为1,![]() 在
在![]() 轴上,
轴上,![]()
-
科目: 来源: 题型:
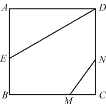
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB,CD上滑动,当CM为何值时,△AED与△CMN相似?
-
科目: 来源: 题型:
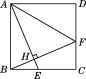
查看答案和解析>>【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求
 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.
(1)点F是DC上一点,连接EF,交AC于点O(如图1),求证:△AOE∽△COF;
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防部迅速派出快艇B追赶(如图1).图2中l1、l2分别表示两船相対于海岸的距离s(海里)与追赶时间t(分)之间的关系.根据图象问答问题:
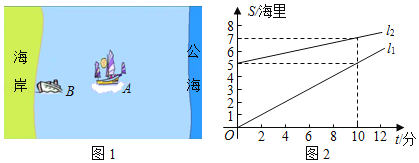
(1)①直线l1与直线l2中 表示B到海岸的距离与追赶时间之间的关系
②A与B比较, 速度快;
③如果一直追下去,那么B (填能或不能)追上A;
④可疑船只A速度是 海里/分,快艇B的速度是 海里/分
(2)l1与l2对应的两个一次函数表达式S1=k1t+b1与S2=k2t+b2中,k1、k2的实际意义各是什么?并直接写出两个具体表达式
(3)15分钟内B能否追上A?为什么?
(4)当A逃离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?为什么?
相关试题

