【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
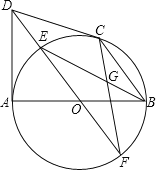
(1)求证:DA=DC;
(2)⊙O的半径为3,DC=4,求CG的长.
参考答案:
【答案】解:(1)证明:连接OC,
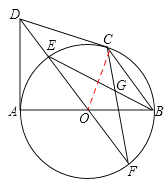
∵DC是⊙O切线,∴OC⊥DC。
∵OA⊥DA,∴∠DAO=∠DCO=90°。
在Rt△DAO和Rt△DCO中,
∵DO=DO,OA=OC,
∴Rt△DAO≌Rt△DCO(HL)。
∴DA=DC.
(2)连接BF、CE、AC,设AC与OD相交于点M,
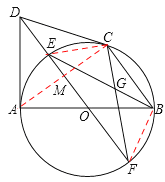
由切线长定理得:DC=DA=4,DO⊥AC,
∴DO平分AC。
在Rt△DAO中,AO=3,AD=4,
由勾股定理得:DO=5。
∵由三角形面积公式得:![]() DAAO=
DAAO=![]() DOAM,
DOAM,
则AM=![]() 。
。
同理CM=AM=![]() 。∴AC=
。∴AC=![]() 。
。
∵AB是直径,∴∠ACB=90°。
由勾股定理得:![]() 。
。
∵由圆周角定理得∠GCB=∠GEF,∠GFE=∠GBC,∴△BGC∽△EGF。
∴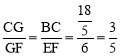 。
。
在Rt△OMC中,CM=![]() ,OC=3,由勾股定理得:OM=
,OC=3,由勾股定理得:OM=![]() 。
。
在Rt△EMC中,CM=![]() ,ME=OE﹣OM=3﹣
,ME=OE﹣OM=3﹣![]() =
=![]() ,由勾股定理得:CE=
,由勾股定理得:CE=![]() 。
。
在Rt△CEF中,EF=6,CE=![]() ,由勾股定理得:CF=
,由勾股定理得:CF=![]() 。
。
∵CF=CG+GF,![]() ,∴CG=
,∴CG=![]() CF=
CF=![]() ×
×![]() =
=![]() 。
。
【解析】
试题分析:(1)连接OC,∠DAO=∠DCO=90°,根据HL证Rt△DAO≌Rt△DCO,根据全等三角形的性质推出即可。
(2)连接BF、CE、AC,由切线长定理求出DC=DA=4,求出DO=5,CM、AM的长,由勾股定理求出BC长,根据△BGC∽△EGF求出![]() ,则CG=
,则CG=![]() CF;利用勾股定理求出CF的长,则CG的长度可求得。
CF;利用勾股定理求出CF的长,则CG的长度可求得。
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?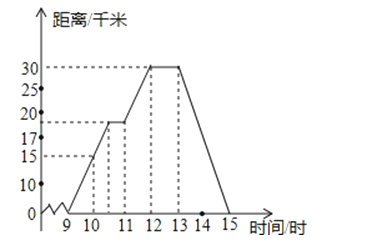
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的是( )
A.经过两点有且只有一条直线
B.三角形的中位线平行且等于第三边的一半
C.平行四边形的对角线相等
D.圆的切线垂直于经过切点的半径 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP∥QR∥ST,则下列各式中正确的是( )

A.∠1+∠2+∠3=180°
B.∠1+∠2﹣∠3=90°
C.∠1﹣∠2+∠3=90°
D.∠2+∠3﹣∠1=180° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:
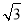 =1.73,结果保留两位有效数字)
=1.73,结果保留两位有效数字)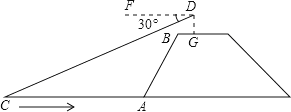
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知xm=2,xn=3,求x2m+3n的值;
(2)先化简,再求值:(a+2b)(a-2b)+(a+2b)2+(2ab2-8a2b2)÷2ab,其中a=1,b=2.
相关试题

