【题目】小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?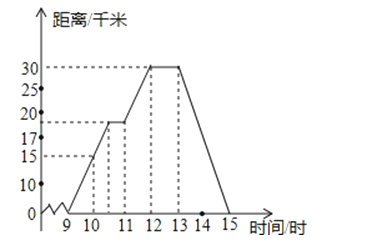
参考答案:
【答案】解:(1)由函数图象,得图象表示了时间、距离的关系,自变量是时间,因变量是距离;
(2)由纵坐标看出10时他距家15千米,13时他距家30千米;
(3)由横坐标看出12:00时离家最远,由纵坐标看出离家30千米;
(4)由纵坐标看出11时距家19千米,12时距家30千米,11时到12时他行驶了30﹣19=11(千米);
(5)由纵坐标看出12:00﹣13:00时距离没变且时间较长,得12:00﹣13:00休息并吃午饭;
(6)由横坐标看出回家时用了2两小时,由纵坐标看出路程是30千米,回家的速度是30÷2=15(千米/小时).
【解析】(1)根据函数图象,可得自变量、因变量;
(2)根据函数图象的纵坐标,可得答案;
(3)根据函数图象的横坐标、纵坐标,可得答案;
(4)根据函数图象的横坐标,可得函数值,根据函数值相减,可得答案;
(5)根据函数图象的纵坐标,可得答案;
(6)根据函数图象的纵坐标,可得距离,根据函数图象的横坐标,可得时间,根据路程除以时间,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?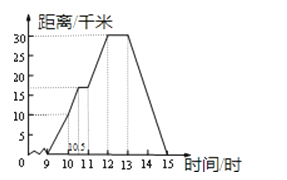
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+4x+k=0有两个相等的实根,则k的值为( )
A.k=﹣4
B.k=4
C.k≥﹣4
D.k≥4 -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某初中每天早上总是在规定时间打开学校大门,七年级同学小明每天早上同一时间从家到学校,周一早上他骑自行车以每小时12千米的速度到校,结果在校门口等了6分钟才开门,周二早上他步行以每小时6千米的速度到校,结果校门已开了12分钟,请解决以下问题:
(1)小明从家到学校的路程是多少千米?
(2)周三早上小明想准时到达学校门口,那么他应以每小时多少千米度速度到学校? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的是( )
A.经过两点有且只有一条直线
B.三角形的中位线平行且等于第三边的一半
C.平行四边形的对角线相等
D.圆的切线垂直于经过切点的半径 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
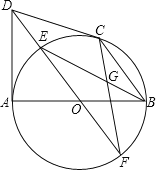
(1)求证:DA=DC;
(2)⊙O的半径为3,DC=4,求CG的长.
相关试题

