【题目】在平面直角坐标系中，已知点A(a，0)、C(0，b)满足，

(1) 直接写出：a＝_________，b＝_________；

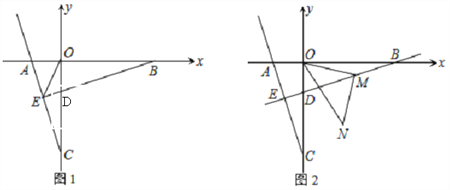
(2) 点B为x轴正半轴上一点，如图1，BE⊥AC于点E，交y轴于点D，连接OE，若OE平分∠AEB，求直线BE的解析式；

(3) 在(2)的条件下，点M为直线BE上一动点，连OM，将线段OM绕点M逆时针旋转90°，如图2，点O的对应点为N，当点M运动时，判断点N的运动路线是什么图形，并说明理由.

参考答案：

【答案】(1) a＝－1，b＝－3；(2)直线BE的解析式为y＝x－1；（3）点N的运动路线是一条直线，解析式为.

【解析】试题分析：（1）根据非负数是性质来求a、b的值；

（2）如图1，过点O作OF⊥OE，交BE于F．构建全等三角形：△EOC≌△FOB（ASA），△AOC≌△DOB（ASA），易求D（0，-1），B（3，0）．利用待定系数法求得直线BE的解析式y=x-1；

（3）如图2，过点M作MG⊥x轴，垂足为G，过点N作NH⊥GH，垂足为H．构建全等三角形：△GOM≌△HMN，故OG=MH，GM=NH．设M（m， m-1），则H（m，-m-1），N（m-1，-m-1），由此求得点N的横纵坐标间的函数关系．

试题解析：(1) a＝－1，b＝－3

(2) 如图1，过点O作OF⊥OE，交BE于F

∵BE⊥AC，OE平分∠AEB

∴△EOF为等腰直角三角形

可证：△EOC≌△FOB（ASA），∴OB＝OC

可证：△AOC≌△DOB（ASA），∴OA＝OD

∵A(－1，0)，B(0，－3)

∴D(0，－1)，B(3，0)

∴直线BD，即直线BE的解析式为y＝x－1

(3) 依题意，△NOM为等腰直角三角形

如图2，过点M作MG⊥x轴，垂足为G，过点N作NH⊥GH，垂足为H

∵△NOM为等腰直角三角形

易证△GOM≌△HMN，

∴OG＝MH，GM＝NH

由(2)知直线BD的解析式y＝x－1

设M(m， m－1)，则H(m， m－1)

∴N(m－1，-m－1)

令(m－1＝x，-m－1＝y，

消去参数m得， -

即直线l的解析式为

关闭