搜索
【题目】从全校1200名学生中随机选取一部分学生进行调查，调查情况：A：上网时间 
小时；B：1小时＜上网时间 
小时；C：4小时＜上网时间 
小时；D：上网时间＞7小时．统计结果制成了如图统计图：
（1）参加调查的学生有人；
（2）请将条形统计图补全；
（3）请估计全校上网不超过7小时的学生人数．
参考答案：
【答案】
（1）200人
（2）解：C的人数是：200﹣20﹣80﹣40=60（人），补图如下：
（3）解：根据题意得： 1200× 
=960（人），
【解析】（1）根据统计图中A的数值求出参加调查的学生的人数；（2）根据条形统计图中A、B、D的人数，求出C的人数，将条形统计图补全；（3）由全校1200名的学生数，求出全校上网不超过7小时的学生人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题1：现有一张△ABC纸片，点D、E分别是△ABC边上两点，若沿直线DE折叠．
（1）探究1：如果折成图①的形状，使A点落在CE上，则∠1与∠A的数量关系是 ；
（2）探究2：如果折成图②的形状，猜想∠1+∠2和∠A的数量关系是 ；
（3）探究3：如果折成图③的形状，猜想∠1、∠2和∠A的数量关系，并说明理由．
（4）问题2：将问题1推广，如图④，将四边形ABCD纸片沿EF折叠，使点A、B落在四边形EFCD的内部时，∠1+∠2与∠A、∠B之间的数量关系是 .
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在边长为4cm正方形 ABCD 中，点P从点A出发，沿AB→BC的路径匀速运动，到点C停止．过点P作PQ∥BD，PQ与边AD（或边CD）交于点Q，PQ的长度y（cm）与点P的运动时图象如图②所示．当P运动2.5s时，PQ的长为（ ）
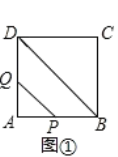
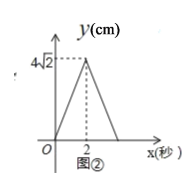
A.
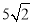cmB.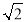
cmC.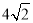
cmD.
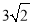cm -
科目： 来源： 题型：
查看答案和解析>>【题目】九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动．在一个不透明的口袋中有三个完全相同的小球，把它们分别标号1、2、3．随机摸出一个小球记下标号后放回摇匀，再从中随机摸出一个小球记下标号．
（1）请用列表或画树形图的方法（只选其中一种），表示两次摸出小球上的标号的所有结果；
（2）规定当两次摸出的小球标号相同时中奖，求中奖的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】某开发商要建一批住房，经调查了解，若甲、乙两队分别单独完成，则乙队完成的天数是甲队的1.5倍；若甲、乙两队合作，则需120天完成．
(1)甲、乙两队单独完成各需多少天？
(2)施工过程中，开发商派两名工程师全程监督，需支付每人每天食宿费150元．已知乙队单独施工，开发商每天需支付施工费为10000元．现从甲、乙两队中选一队单独施工，若要使开发商选甲队支付的总费用不超过选乙队的，则甲队每天的施工费最多为多少元？(总费用＝施工费＋工程师食宿费)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°．E、F分别是BC、CD上的点．且∠EAF＝60°．探究图中线段BE、EF、FD之间的数量关系．
小王同学探究此问题的方法是，延长FD到点G，使DG＝BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 ；
探索延伸：
如图2，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°．E、F分别是BC、CD上的点，且∠EAF＝
∠BAD，上述结论是否仍然成立，并说明理由；实际应用：
如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，有一个水池，其底面是边长为16尺的正方形，一根芦苇AB生长在它的正中央，高出水面部分BC的长为2尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′，则这根芦苇AB的长是（ ）
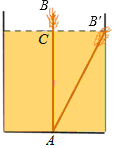
A. 15尺B. 16尺C. 17尺D. 18尺
相关试题
