【题目】如图所示,点![]() 分别是
分别是![]() 平分线上的点,
平分线上的点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
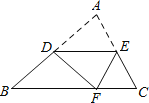
于点![]() ,下列结论错误的是( )
,下列结论错误的是( )
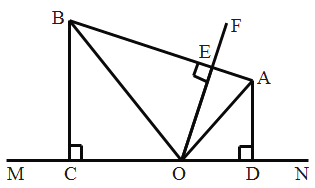
A.![]()
B.![]()
C.点![]() 是
是![]() 的中点
的中点
D.图中与![]() 互余的角有两个
互余的角有两个
参考答案:
【答案】D
【解析】
根据角分线的定义,可证![]() ;
;
根据角平分线上的点到角两边距离相等可证![]() ;
;
通过证明![]() 和
和![]() 可得OD=OE=OC;
可得OD=OE=OC;
通过同角或等角的余角相等,可证明与![]() 互余的角有四个.由此可判断.
互余的角有四个.由此可判断.
解:∵点A,B分别是∠NOF,∠MOF平分线上的点
∴![]()
∴![]()
即![]() ,故A正确;
,故A正确;
又∵![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]()
∴![]()
∴![]() ,故B选项正确;
,故B选项正确;
在Rt△AOD和Rt△AOE中,
![]()
∴![]()
∴OD=OE,∠OAE=∠OAD
同理可证OC=OE
∴OC= OD,即O为CD的中点,故C正确;
∵![]() 于点
于点![]() ,
,
∴∠COB+∠CBO=90°,
又∵![]() ,
,
∴∠BOE+∠CBO=90°,
∵![]() ,
,![]() 于点
于点![]()
∴∠BOE+∠AOE=90°,∠OAE+∠AOE=90°
∴∠BOE=∠OAE=∠OAD
∴∠OAE +∠CBO=90°,∠OAD +∠CBO=90°
所以与∠CBO互余的角有四个,分别为∠COB,∠BOE,∠OAE,∠OAD,D选项错误;
故选D.
-
科目: 来源: 题型:
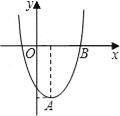
查看答案和解析>>【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标为(﹣6,6),以A为顶点的∠BAC的两边始终与x轴交于B、C两点(B在C左面),且∠BAC=45°.
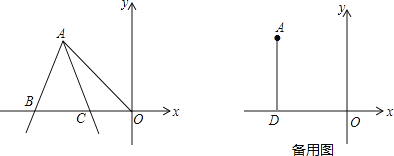
(1)如图,连接OA,当AB=AC时,试说明:OA=OB.
(2)过点A作AD⊥x轴,垂足为D,当DC=2时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=kx+b的图象经过点(0,﹣2),(3,1).
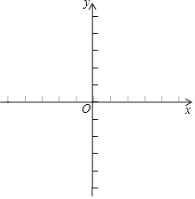
(1)求一次函数的表达式,并在所给直角坐标系中画出此函数的图象;
(2)根据图象回答:当x 时,y1=0;
(3)求直线y1=kx+b、直线y2=﹣2x+4与y轴围成的三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=70°∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】)图①中是一座钢管混凝土系杆拱桥,桥的拱肋ACB可视为抛物线的一部分(如图②),桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋
的跨度AB为200米,与AB中点O相距20米处有一高度为48米的系杆.
【1】求正中间系杆OC的长度;
【2】若相邻系杆之间的间距均为5米(不考虑系杆的粗细),则是否存在一根系杆的长度恰好是OC长度的一半?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年,在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.(售价不低于进价).请根据小丽提供的信息,解答小华和小明提出的问题.

认真阅读上面三位同学的对话,请根据小丽提供的信息.
(1)解答小华的问题;
(2)解答小明的问题.
相关试题

