【题目】小邢和小华相约放学后去公园跑步,她们一起以4km/h的速度从学校出发,走了15分钟后小邢发现忘了带作业,就以5km/h的速度回学校去拿,到达学校后,又用了6分钟取作业,之后便以同样的速度去追赶小华,结果在距公园3km处追上了小华,试求学校与公园的距离.
参考答案:
【答案】学校与公园的距离为14km.
【解析】
根据路程=速度×时间,计算出走了15分钟后,二者与学校的距离,根据时间=路程÷速度,计算出小邢返回学校所用的时间,两段时间相加,就是二者分开后小华走的时间,根据小华走的速度和时间,计算出二者分开后小华走的距离,设小邢追上小华所用的时间为th,根据二者的速度,时间,路程之间的关系,列出关于t的一元一次方程,解之,求出这段时间小华走的距离,四段距离之和即为学校与公园的距离,即可得到答案.
解:根据题意得:
走了15分钟后,二者与学校的距离为:4×![]() =1(km),
=1(km),
小邢返回学校所用的时间t1=![]() =0.2h,
=0.2h,
二者分开后小华走的时间为t2=0.2+![]() =0.3(h),
=0.3(h),
二者分开后小华走的距离为:4×0.3=1.2(km),
设小邢追上小华所用的时间为th,
根据题意得:
5t=4t+1+1.2,
解得:t=2.2,
这段时间小华走的距离为:4×2.2=8.8(km),
学校与公园的距离为:8.8+1+1.2+3=14(km),
答:学校与公园的距离为14km.
-
科目: 来源: 题型:
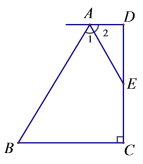
查看答案和解析>>【题目】如图,已知AD∥BC,DC⊥BC, AE平分∠BAD, E为CD中点,试探索AD、BC和AB之间有何关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:数和形是数学的两个主要研究对象,我们经常运用数形结合,树形转化的方法解决一些数学问题,小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:P1P2=
 ,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=
,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x= ,y=
,y= .
.启发应用:
如图3:在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A,B,
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由;
(3)若∠BOA的平分线交AB于点N,交⊙M于点E,分别求出OE的表达式y1,过点M的反比例函数的表达式y2,并根据图象,当y2>y1>0时,请直接写出x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形。
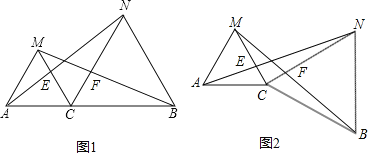
(1)△ACN≌△MCB吗?为什么?
(2)证明:CE=CF;
(3)若△CBN绕着点C旋转一定的角度(如图2),则上述2个结论还成立吗?
(4)若AN、MB相交于O,则∠AOB度数有没变化?若没有变化,则∠AOB= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=
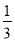 OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )

A. 10cm B. 12cm C. 15cm D. 17cm
-
科目: 来源: 题型:
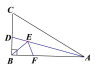
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=6, ∠BAC=30, ∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是___
相关试题

