【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
![]() 利用图中条件,求
利用图中条件,求![]() 的值并求出反比例函数和一次函数的解析式;
的值并求出反比例函数和一次函数的解析式;
![]() 根据图象直接写出
根据图象直接写出![]() 时
时![]() 的取值范围;
的取值范围;
![]() 求
求![]() 的面积.
的面积.

参考答案:
【答案】![]() ,
,![]() ;
;![]()
![]() 或
或![]() ;
;![]() .
.
【解析】
(1)把A坐标代入反比例解析式求出m的值,确定出反比例解析式,再将B坐标代入反比例解析式求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)根据一次函数与反比例函数的交点坐标,结合图形,找出满足题意不等式的解集即可;
(3)对于一次函数,确定出C与D坐标,三角形AOB面积=三角形AOC面积+三角形COD面积+三角形BOD面积,求出即可.
![]() 把
把![]() 代入反比例解析式得:
代入反比例解析式得:![]() ,即反比例解析式为
,即反比例解析式为![]() ,
,
把![]() 代入反比例解析式得:
代入反比例解析式得:![]() ,即
,即![]() ,
,
把![]() 与
与![]() 代入一次函数解析式得:
代入一次函数解析式得:![]() ,
,
解得:![]() ,
,
则一次函数解析式为![]() ;
;
![]() ∵一次函数与反比例函数的交点为
∵一次函数与反比例函数的交点为![]() ,
,![]() ,
,
∴由图象得:![]() 时
时![]() 的取值范围为
的取值范围为![]() 或
或![]() ;
;
![]() 对于一次函数
对于一次函数![]() ,
,
令![]() ,得到
,得到![]() ;令
;令![]() ,得到
,得到![]() ,即
,即![]() ,
,![]() ,
,
∴![]() ,
,
则![]() .
.
-
科目: 来源: 题型:
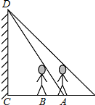
查看答案和解析>>【题目】墙壁
 处有一盏灯(如图),小明站在
处有一盏灯(如图),小明站在 处测得他的影长与身长相等都为
处测得他的影长与身长相等都为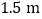 ,小明向墙壁走
,小明向墙壁走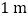 到
到 处发现影子刚好落在A
处发现影子刚好落在A 点,则灯泡与地面的距离
点,则灯泡与地面的距离 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店计划购进
 ,
,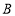 两种笔记本共60本,每本
两种笔记本共60本,每本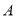 种笔记本比
种笔记本比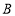 种笔记本的利润高3元,销售2本
种笔记本的利润高3元,销售2本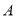 种笔记本与3本
种笔记本与3本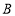 种笔记本所得利润相同,其中
种笔记本所得利润相同,其中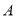 种笔记本的进货量不超过进货总量的
种笔记本的进货量不超过进货总量的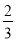 ,
,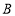 种笔记本的进货量不少于30本.
种笔记本的进货量不少于30本.(1)每本
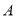 种笔记本与
种笔记本与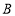 种笔记本的利润各为多少元?
种笔记本的利润各为多少元?(2)设购进
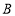 种笔记本
种笔记本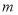 本,销售总利润为
本,销售总利润为 元,文具店应如何安排进货才能使得
元,文具店应如何安排进货才能使得 最大?
最大?(3)实际进货时,
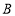 种笔记本进价下降
种笔记本进价下降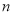 (
(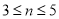 )元.若两种笔记本售价不变,请设计出笔记本销售总利润最大的进货方案.
)元.若两种笔记本售价不变,请设计出笔记本销售总利润最大的进货方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个矩形的短边与长边的比值为
 (黄金分割数),我们把这样的矩形叫做黄金矩形.
(黄金分割数),我们把这样的矩形叫做黄金矩形. 操作:请你在如图所示的黄金矩形
操作:请你在如图所示的黄金矩形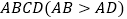 中,以短边
中,以短边 为一边作正方形
为一边作正方形 ;
; 探究:在
探究:在 中的四边形
中的四边形 是不是黄金矩形?若是,请予以证明;若不是,请说明理由.
是不是黄金矩形?若是,请予以证明;若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知平面内一点
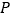 与一直线
与一直线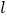 ,如果过点
,如果过点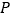 作直线
作直线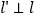 ,垂足为
,垂足为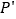 ,那么垂足
,那么垂足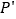 叫做点
叫做点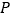 在直线
在直线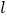 上的射影;如果线段
上的射影;如果线段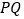 的两个端点
的两个端点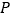 和
和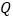 在直线
在直线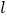 上的射影分别为点
上的射影分别为点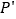 和
和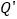 ,那么线段
,那么线段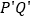 叫做线段
叫做线段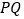 在直线
在直线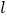 上的射影.
上的射影.如图①,已知平面内一点
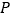 与一直线
与一直线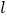 ,如果过点
,如果过点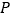 作直线
作直线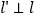 ,垂足为
,垂足为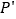 ,那么垂足
,那么垂足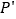 叫做点
叫做点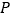 在直线
在直线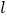 上的射影;如果线段
上的射影;如果线段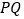 的两个端点
的两个端点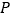 和
和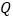 在直线
在直线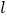 上的射影分别为点
上的射影分别为点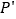 和
和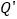 ,那么线段
,那么线段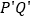 叫做线段
叫做线段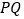 在直线
在直线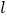 上的射影.
上的射影.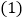 如图②,
如图②,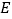 、
、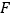 为线段
为线段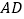 外两点,
外两点,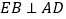 ,
,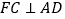 ,垂足分别为
,垂足分别为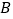 、
、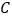 .
.则
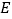 点在
点在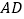 上的射影是________点,
上的射影是________点,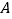 点在
点在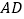 上的射影是________点,
上的射影是________点,线段
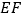 在
在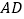 上的射影是________,线段
上的射影是________,线段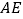 在
在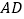 上的射影是________;
上的射影是________;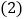 根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)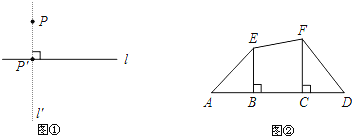
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
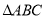 中,
中,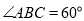 ,点
,点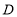 ,
,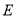 分别为
分别为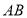 ,
,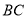 上一点,
上一点,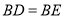 ,连接
,连接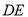 ,
,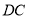 ,
,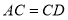 .
.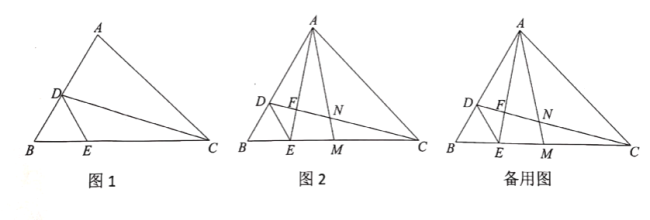
(1)如图1,若
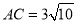 ,
,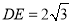 ,求
,求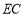 的长;
的长;(2)如图2,连接
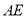 交
交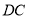 于点
于点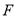 ,点
,点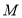 为
为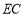 上一点,连接
上一点,连接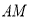 交
交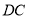 于点
于点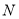 ,若
,若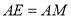 ,求证:
,求证: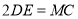 ;
;(3)在(2)的条件下,若
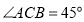 ,直接写出线段
,直接写出线段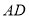 ,
,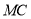 ,
,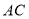 的等量关系.
的等量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=15,AC=20,BC边上的高AD=12,则BC的长为( )
A.25B.7C.25或7D.14或4
相关试题

