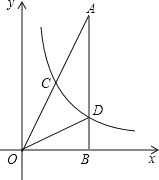
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=![]() 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)求反比例函数解析式;
(2)求点C的坐标.
参考答案:
【答案】(1)反比例函数解析式为y=![]() ;
;
(2)C点坐标为(2,4)
【解析】
试题(1)由S△BOD=4可得BD的长,从而可得D的坐标,然后代入反比例函数解析式可求得K,从而得解析式为y=![]() ;
;
(2)由已知可确定A点坐标,再由待定系数法求出直线AB的解析式为y=2x,然后解方程组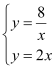 即可得到C点坐标.
即可得到C点坐标.
试题解析:(1)∵∠ABO=90°,OB=4,S△BOD=4,
∴![]() OB×BD=4,解得BD=2,
OB×BD=4,解得BD=2,
∴D(4,2)
将D(4,2)代入y=![]()
得2=![]()
∴k=8
∴反比例函数解析式为y=![]() ;
;
(2)∵∠ABO=90°,OB=4,AB=8,
∴A点坐标为(4,8),
设直线OA的解析式为y=kx,
把A(4,8)代入得4k=8,解得k=2,
∴直线AB的解析式为y=2x,
解方程组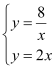 得
得![]() 或
或![]() ,
,
∴C点坐标为(2,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:

①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是双曲线y=﹣
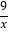 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=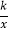 上运动,则k的值为_____.
上运动,则k的值为_____.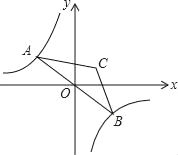
-
科目: 来源: 题型:
查看答案和解析>>【题目】在3×3的方格中,每行、每列及对角线上的3个代数式的和都相等,我们把这样的方格图叫做“等和格”。如图的“等和格”中,每行、每列及对角线上的3个代数式的和都等于15.
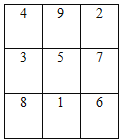
(1)图1是显示部分代数式的“等和格”,可得a=_______(含b的代数式表示);
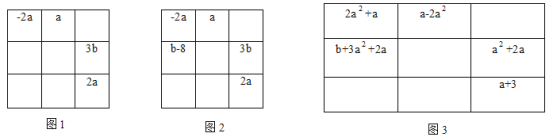
(2)图2是显示部分代数式的“等和格”,可得a=__________,b=__________;
(3)图3是显示部分代数式的“等和格”,求b的值。(写出具体求解过程)
-
科目: 来源: 题型:
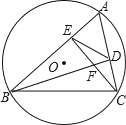
查看答案和解析>>【题目】如图,⊙O的半径为2,弦BC=2
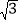 ,点A是优弧BC上一动点(不包括端点),△ABC的高BD、CE相交于点F,连结ED.下列四个结论:
,点A是优弧BC上一动点(不包括端点),△ABC的高BD、CE相交于点F,连结ED.下列四个结论:①∠A始终为60°;
②当∠ABC=45°时,AE=EF;
③当△ABC为锐角三角形时,ED=
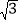 ;
;④线段ED的垂直平分线必平分弦BC.
其中正确的结论是_____.(把你认为正确结论的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:
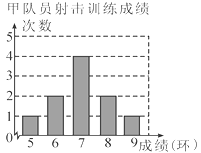
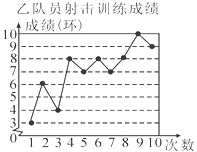
根据以上信息,整理分析数据如下:
平均成绩(环)
中位数(环)
众数(环)
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】近期,我市持续出现雾霾天气,给广大市民的工作和生活造成了严重的影响.为此,“雾霾天气的主要成因”就成为了某校环保小组调查研究的课题,他们随机调查了部分市民,并对调查结果进行了整理,绘制了如图所示的不完整的统计图表.请根据图表中提供的信息解答下列问题:
级别
观点
频数(人数)
A
大气气压低,空气不流动
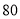
B
地面灰尘大,空气湿度低
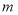
C
汽车尾部排放
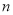
D
工厂造成污染
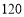
E
其他
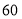
调查结果扇形统计图
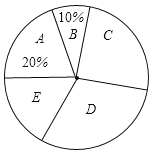
(1)填空:
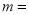 ______,
______,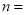 ______;
______;(2)求出扇形统计图中E组所占的百分比以及扇形统计图中区域D所对应的扇形圆心角度数;
相关试题

