【题目】在△ABC中,AB=AC,AB>BC,点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC,若△ABC的面积为18,则△ABE与△CDF的面积之和是( )

A.6B.8C.9D.12
参考答案:
【答案】D
【解析】
先根据△ABD与△ADC等高,底边值为1:2,得出△ABD与△ADC面积比为1:2,再证△ABE≌△CAF,即可得出△ABE和△CDF的面积和,即可选出答案.

∵在等腰△ABC中,AB=AC,CD=2BD,
∴△ABD与△ADC等高,底边比值为1:2
∴△ABD与△ADC的面积比为1:2,
∵△ABC的面积为18
∴△ABD的面积为6,△ADC的面积为12,
∵∠1=∠2,
∴∠BEA=∠AFC
∵∠1=∠3+∠ABE,∠3+∠4=∠BAC,∠BAC=∠1
∴∠ABE=∠4
∴△ABE≌△ACF(AAS)
∴△ABE与△ACF的面积相等,
∴△ABE与△CDF的面积和等于△ACF与△CDF的面积和
即△ADC的面积12
故答案选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y=
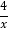 图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=
图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=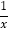 的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.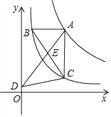
-
科目: 来源: 题型:
查看答案和解析>>【题目】为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家园林公司承接了某项园林绿化工程,己知乙公司单独完成此项工程所需要的天数是甲公司单独完成所需要天数的1.5倍,如果甲公司先单独工作10天,再由乙公司单独工作l5天,这样恰好完成整个工程的
 ;
;(1)求甲、乙两公司单独完成这项工程各需多少天?
(2)园林部门要求完成该绿化工程的时间不得超过30天,甲、乙公司合作若干天后,甲公司另有项目离开,剩下的工程由乙公司单独完成,求甲、乙两公司至少合作多少天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:
(1)如图:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC.CD上的点且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE连结AG,先证明△ABE≌△ADG.再证明____≌____,可得出结论,他的结论应是____.请你按照小王同学的思路写出完整的证明过程.

实际应用
(2)如图,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处.且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离是 海里(直接写出答案)

相关试题

