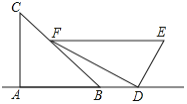
【题目】善于思考的小鑫同学,在一次数学活动中,将一副直角三角板如图放置,![]() ,
,![]() ,
,![]() 在同一直线上,且
在同一直线上,且![]() ,
,![]() ,
,![]() ,
,![]() ,量得
,量得![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】![]()
【解析】
过F作FH垂直于AB,得到∠FHB为直角,进而求出∠EFD的度数为30°,利用30°角所对的直角边等于斜边的一半求出EF的长,再利用勾股定理求出DF的长,由EF与AD平行,得到内错角相等,确定出∠FDA为30°,再利用30°角所对的直角边等于斜边的一半求出FH的长,进而利用勾股定理求出DH的长,由DH-BH求出BD的长即可.
解:过点F作FH⊥AB于点H,
∴∠FHB=90°,
∵∠EDF=90°,∠E=60°,
∴∠EFD=90°-60°=30°,
∴EF=2DE=24,
∴![]() ,
,
∵EF∥AD,
∴∠FDA=∠DFE=30°,
∴![]() ,
,
∴![]() ,
,
∵△ABC为等腰直角三角形,
∴∠ABC=45°,
∴∠HFB=90°-45°=45°,
∴∠ABC=∠HFB,
∴![]() ,
,
则BD=DH-BH=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校初中各年级学生每天的平均睡眠时间(单位:
 ,精确到
,精确到 ,抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
,抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数
 的值为_____,所抽查的学生人数为______.
的值为_____,所抽查的学生人数为______.(2)求出平均睡眠时间为8小时的人数,并补全条形统计图.
(3)求出这部分学生的平均睡眠时间的众数和平均数.
(4)如果该校共有学生1800名,请你估计睡眠不足(少于8小时)的学生数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,二次函数
 的图象与坐标轴交于
的图象与坐标轴交于 ,
,  ,
,  三点,其中点
三点,其中点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,连接
,连接 ,
,  .动点
.动点 从点
从点 出发,在线段
出发,在线段 上以每秒
上以每秒 个单位长度的速度向点
个单位长度的速度向点 作匀速运动;同时,动点
作匀速运动;同时,动点 从点
从点 出发,在线段
出发,在线段 上以每秒
上以每秒 个单位长度的速度向点
个单位长度的速度向点 作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为
作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为 秒.连接
秒.连接 .
.(
 )填空:
)填空: 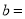 __________,
__________,  __________.
__________.(
 )在点
)在点 ,
,  运动过程中,
运动过程中,  可能是直角三角形吗?请说明理由.
可能是直角三角形吗?请说明理由.(
 )在
)在 轴下方,该二次函数的图象上是否存在点
轴下方,该二次函数的图象上是否存在点 ,使
,使 是以点
是以点 为直角顶点的等腰直角三角形?若存在,请求出运动时间
为直角顶点的等腰直角三角形?若存在,请求出运动时间 ;若不存在,请说明理由.
;若不存在,请说明理由.(
 )如图②,点
)如图②,点 的坐标为
的坐标为 ,线段
,线段 的中点为
的中点为 ,连接
,连接 ,当点
,当点 关于直线
关于直线 的对称点
的对称点 恰好落在线段
恰好落在线段 上时,请直接写出点
上时,请直接写出点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
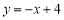 过点
过点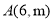 且与
且与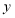 轴交于点
轴交于点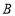 ,把点
,把点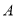 向左平移2个单位,再向上平移4个单位,得到点
向左平移2个单位,再向上平移4个单位,得到点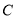 .过点
.过点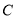 且与
且与 平行的直线交
平行的直线交 轴于点
轴于点 .
.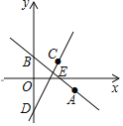
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少万元?
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.
(1)求y关于x的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为s(千米).请直接写出s关于x的表达式;
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为a(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度a.在下图中画出乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象.
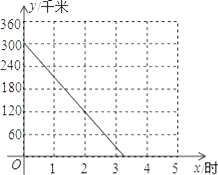
-
科目: 来源: 题型:
查看答案和解析>>【题目】P是三角形ABC内一点,射线PD∥AC,射线PE∥AB.
(1)当点D,E分别在AB,BC上时,
①补全图1;
②猜想∠DPE与∠A的数量关系,并证明;
(2)当点D,E都在线段BC上时,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

相关试题

